Hello coders!! In this article, we will be learning about NumPy sin in Python. We will be looking into certain examples and will use the function in different ways. So, without wasting any moment, let us begin.
Syntax:
It is a mathematical function, used to calculate the trigonometric sine for all x, where x is an array.
numpy.sin(x[, out]) = ufunc ‘sin’)
Parameters:
- array: array elements in radians.
2pi Radians = 360 degrees
Return Value:
- An array with trigonometric sine of x for all x
Does numpy sin take radians or degrees?
The np.sin() function help to find the sine value of the angle in degree and radian. To get the sine value of the angle in radians, need to multiply the angle with np.pi/180.
Illustrated Examples:
example 1: Numpy sin with a single value:
np.sin(np.pi/2.)
1.0
As you can see, we calculated the value of sin(pi/2) using the sin() method of the NumPy module.
example 2: with an array of values:
import numpy as np
inp = [0, np.pi / 2, np.pi / 3, np.pi]
print ("Input array : \n", inp)
opt = np.sin(inp)
print ("\nSine values : \n", opt)

In this example, we have used an array of elements as input. The different elements are:
- 0
- pi / 2
- np.pi / 3
- pi
We have then used the np sin method to calculate the sin value of all the corresponding elements. As said earlier, this method gives the sin value of each element of the array, thus giving the output as:
- 0.00000000e+00
- 1.00000000e+00
- 8.66025404e-01
- 1.22464680e-16
Example 4: numpy sin degrees:
np.sin(np.deg2rad(90))
1.0
To use the angles in degrees rather than radians, we have used the np.deg2rad() method. This method is used to convert angles from degrees to radians.
Syntax:
numpy.deg2rad(x[, out]) = ufunc ‘deg2rad’)
example 5: numpy sin squared:
import numpy as np
inp = [0, np.pi / 2, np.pi / 3, np.pi]
print ("Input array : \n", inp)
opt = np.sin(in_array) ** 2
print ("\nSine Square values : \n", opt)

In this example, we have squared the sine values by raising it to power 2 and stored the output in an array. We then printed the array to get the desired output.
example 6: np sin fit:
from scipy import optimize
x_data = np.linspace(-5, 5, num=50)
y_data = 2.9 * np.sin(1.5 * x_data) + np.random.normal(size=50)
def test_func(x, a, b):
return a * np.sin(b * x)
pars, pars_co = optimize.curve_fit(test_func, x_data, y_data, p0=[2, 2])
plt.figure(figsize=(6, 4))
plt.scatter(x_data, y_data, label='Data')
plt.plot(x_data, test_func(x_data, pars[0], pars[1]))
plt.show()
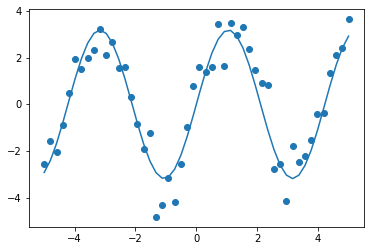
As you can see, in this example, we have used the numpy functions to create the data. We then used the sin method for the value of the y-axis. We then optimize the curve and fit the sine curve to get the desired output.
example 7: numpy generate sin wave plot:
import numpy as np
import matplotlib.pyplot as plt
inp = np.linspace(-np.pi, np.pi, 12)
opt = np.sin(inp)
plt.plot(inp, opt, color = 'green', marker = "o")
plt.title("numpy.sin()")
plt.show()
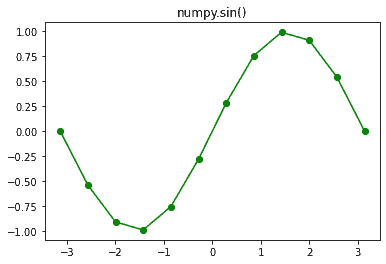
Here, we have plotted the sine graph using the sin method, thus getting the sine graph as output.
Python np sin inverse:
numpy.arcsin() function helps user to calculate inverse sine for all x.
Syntax:
numpy.arcsin(x[, out]) = ufunc ‘arcsin’)
Parameters:
- array : elements in radians
- out : array of same shape as x.
Return Value:
- An array with inverse sine of x.
import numpy as np
inp = [0, 1, 0.3, -1]
print ("Input array : \n", inp)
opt = np.arcsin(inp)
print ("\nInverse Sine values : \n", opt)
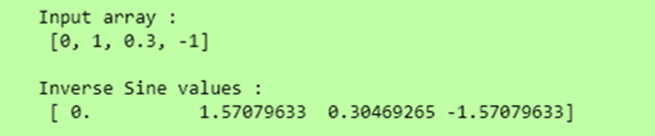
In this example, we have used the np.arcsin() method to find the inverse sin value of the elements of the array.
Numpy sin vs Math sin:
math.sin works on a single number, the numpy version works on numpy arrays and is tremendously faster due to the benefits of vectorization.
| Math Sin | NumPy Sin |
| works on a single number | works on numpy arrays |
| relatively slower | tremendously faster due to the benefits of vectorization |
| Syntax: math.sin(x) x -> The number to find the sine of | Syntax: numpy.sin(x[, out]) = ufunc ‘sin’) array -> array elements in radians. |
import math | import numpy as np |
| 0.49999999999999994 1.0 | [0.00000000e+00 1.00000000e+00 8.66025404e-01 1.22464680e-16] |
Must Read
Conclusion:
With this, we come to an end with this article. I hope that this article clarified the concept of NumPy sin.
However, if you have any doubts or questions, do let me know in the comment section below. I will try to help you as soon as possible.
Happy Pythoning!
