The Numpy module of python is the toolkit. Because it is a function to perform various operations, these operations are high scientific computations in python. Numpy supports multiple dimensions. The toolkits work on them. An array in numpy can be one dimension and two, three, or higher. Thus we have a quick review. As of now, we will read about the numpy tanh. An easy function to use and understand the trigonometric functions.
What Exactly is Numpy tanh?
This function is used to calculate the hyperbolic tangent for all the elements of the array passed as the argument. Here x(being the array elements).
Note: The numpy tanh compute hyperbolic tangent element-wise.
Syntax Numpy tanh
The standard syntax of the Function numpy tanh is:
numpy.tanh(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'tanh'>
Which is equivalent to in terms of mathematics
np.sinh(x)/np.cosh(x)or-1j * np.tan(1j*x).
In other simple way the syntax of tanh can be written as:
numpy.tanh(x[, out])
Parameters Used with numpy tanh:
| Parameters | Mandatory or not |
| x | mandatory |
| out | optional |
| where | optional |
| casting | optional |
| order | optional |
| subok | optional |
| dtype | optional |
| signature | optional |
x : array_like
This parameter isInput values whose square-roots have to be determined. In other words, it specifies the radicand. The radicand is the value under the radical when you compute the square root.
out
The ‘out’ keyword argument expects to be a tuple with one entry per output (which can be None for arrays to be allocated by the ufunc). The out parameter enables you to specify an array where the output will be stored. This parameter is not used in simpler calculations but at a higher level. This parameter provides a location to store the result. If provided, it must have a shape for the inputs broadcast. A freshly-allocated array returned if not provided or None. A tuple (possible only as a keyword argument) must have a length equal to the number of outputs.
where
This parameter Accepts a boolean array, which is broadcast together with the operands. Values of True indicate that to calculate the ufunc at that position and False values indicate to leave the value in the output alone. Generalized ufuncs cannot use this argument because those take non-scalar input.
order
This parameter specifies the calculation iteration order/memory layout output array. Defaults to ‘K.’ ‘C’ means the output should be C-contiguous, ‘F’ means F-contiguous, ‘A’ means F-contiguous if the inputs are F-contiguous and not also not C-contiguous
signature
This argument allows you to provide a specific signature for the 1-d loop to use in the underlying calculation. If the loop specified does not exist for the ufunc, then a TypeError is raised. Usually, a suitable loop is found automatically by comparing the input types with what is available and searching for a loop with data-types. The types attribute of the ufunc object provide a list of known signatures.
Still, there are more parameters to mention. But you do not need to know all. To know all we need to see the unfunc docs. So you would get an idea of all the parameters.
Returning Value
As per NumPy.org, an array with the hyperbolic tangent of x for all x i.e. array elements. Which is basically the corresponding hyperbolic tangent values.
When will Numpy tanh Return Value Error
ValueError: invalid return array shape
if out is provided and out.shape != x.shape
Examples to Comprehend tanh
Now we import the module first
import numpy as np
Now using numpy in a better way.
import math
in_array = [0, math.pi / 2, np.pi / 3, np.pi]
print ("Input array : \n", in_array)
Input array :
[0, 1.5707963267948966, 1.0471975511965976, 3.141592653589793]
tanh_Values = np.tanh(in_array)
print ("\nTangent Hyperbolic values : \n", tanh_Values)
Tangent Hyperbolic values :
[ 0. 0.91715234 0.78071444 0.99627208]
Here we also used the dtype parameter to fix datatype. This example also shows that it retains the dimensionality of the original array.
# Example of providing the optional output parameter illustrating
# that what is returned is a reference to said parameter
out1 = np.array([0], dtype='d')
out2 = np.tanh([0.1], out1)
out2 is out1
True
Now we will see graphical plotting of this
in_array = np.linspace(-np.pi, np.pi, 12)
out_array = np.tanh(in_array)
print("in_array : ", in_array)
in_array : [-3.14159265 -2.57039399 -1.99919533 -1.42799666 -0.856798 -0.28559933
0.28559933 0.856798 1.42799666 1.99919533 2.57039399 3.14159265]
print("\nout_array : ", out_array)
out_array : [-0.99627208 -0.98836197 -0.96397069 -0.89125532 -0.69460424 -0.27807943
0.27807943 0.69460424 0.89125532 0.96397069 0.98836197 0.99627208]
# red for numpy.tanh()
plt.plot(in_array, out_array, color = 'red', marker = "o")
plt.title("numpy.tanh()")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
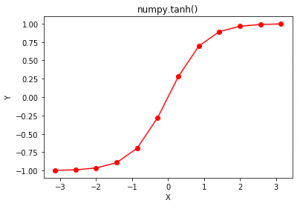
All the examples give the idea of using the function. Now you are ready to go.
What’s Next?
NumPy is mighty and incredibly essential for information science in Python. That being true, if you are interested in data science in Python, you really ought to find out more about Python.
You might like our following tutorials on numpy.
- Mean: Implementation and Importance
- Using Random Function to Create Random Data
- Reshape: Reshaping Arrays With Ease
- In-depth Explanation of np.power() With Examples
- Clip Function
Real World Applications
- Machine Learning
- Neural Network
Conclusion
In conclusion, the numpy tanh function is useful for hard calculations. Those computations can be of broader aspects—both primary and scientific as well.
Still have any doubts or questions, do let me know in the comment section below. I will try to help you as soon as possible.
Happy Pythoning!
