Implementing Dijkstra’s Algorithm in Python

Whenever we need to represent and store connections or links between elements, we use data structures known as graphs. In a graph, we have nodes (vertices) and edges. Nodes are objects (values), and edges are the lines that connect nodes. In python, we represent graphs using a nested dictionary. We represent nodes of the graph as the key and its connections as the value. We often need to find the shortest distance between these nodes, and we generally use Dijkstra’s Algorithm in python.  A graph in general looks like this-

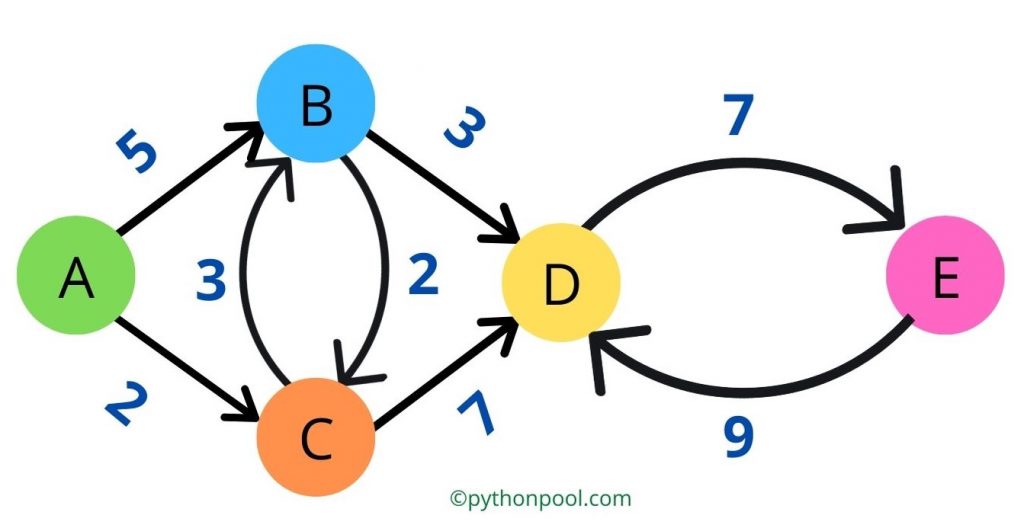
So, Dijkstra’s Algorithm is used to find the shortest distance between the source node and the target node. The approach that Dijkstra’s Algorithm follows is known as the Greedy Approach. Although today’s point of discussion is understanding the logic and implementation of Dijkstra’s Algorithm in python, if you are unfamiliar with terms like Greedy Approach and Graphs, bear with us for some time, and we will try explaining each and everything in this article. 

Concept Behind Dijkstra’s Algorithm 

What is Greedy Approach? 

In the Introduction section, we told you that Dijkstra’s Algorithm works on the greedy approach, so what is this Greedy approach?

In Laymen’s terms, the Greedy approach is the strategy in which we chose the best possible choice available, assuming that it will lead us to the best solution.  

Think about it in this way, we chose the best solution at that moment without thinking much about the consequences in the future.  

Dijkstra’s Algorithm Description

Step 1: Make a temporary graph that stores the original graph’s value and name it as an unvisited graph. Also, initialize a list called a path to save the shortest path between source and target. 

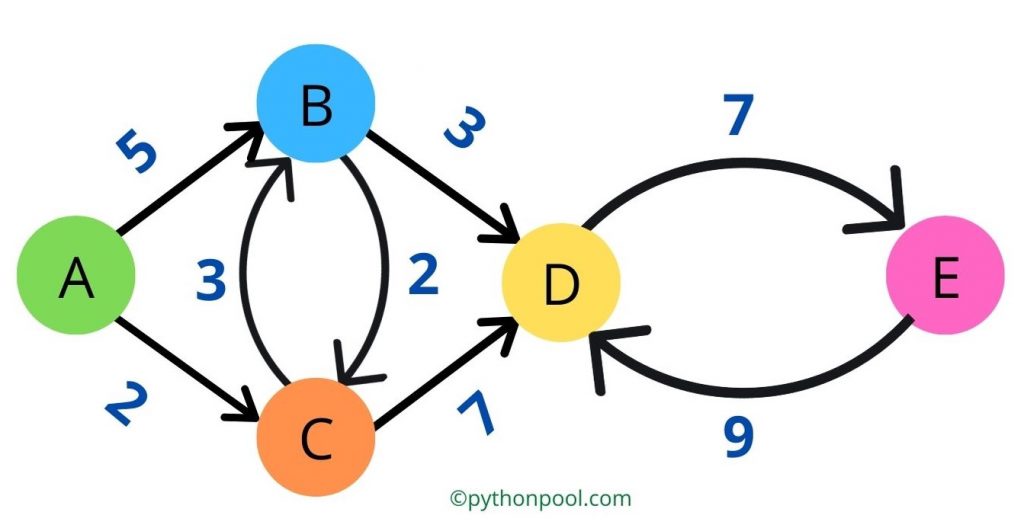
Step 2: We need to calculate the Minimum Distance from the source node to each node.

Initially, mark total_distance for every node as infinity (∞) and the source node mark total_distance as 0, as the distance from the source node to the source node is 0. Also, mark this source node as current_node. 

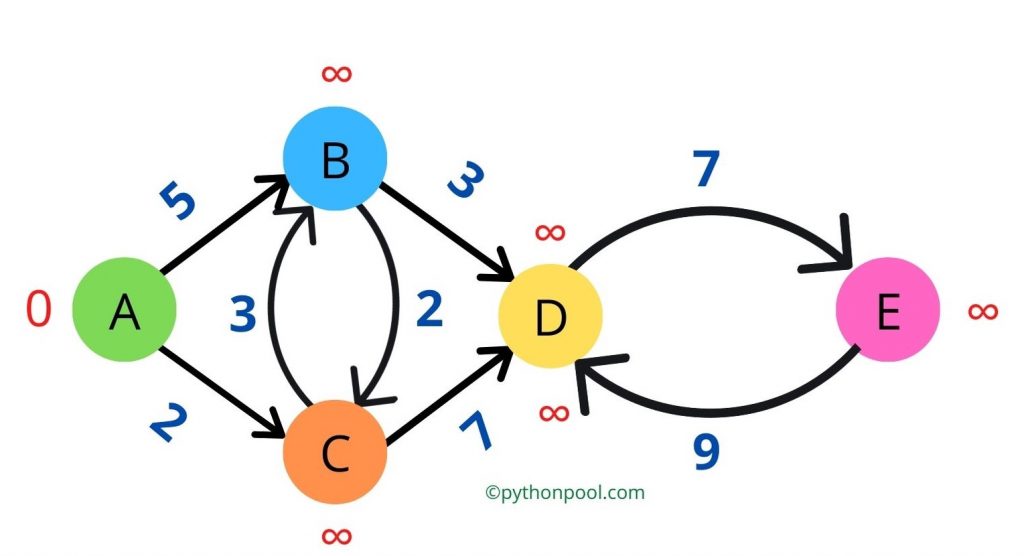
Step 3: From the current_node, select the neighbor nodes (nodes that are directly connected) in any random order. Check if the current value of that node is (initially it will be (∞)) is higher than (the value of the current_node + value of the edge that connects this neighbor node with current_node ).

If yes, then replace the importance of this neighbor node with the value of the current_node + value of the edge that connects this neighbor node with current_node. Repeat this process for all the neighboring nodes of the current node

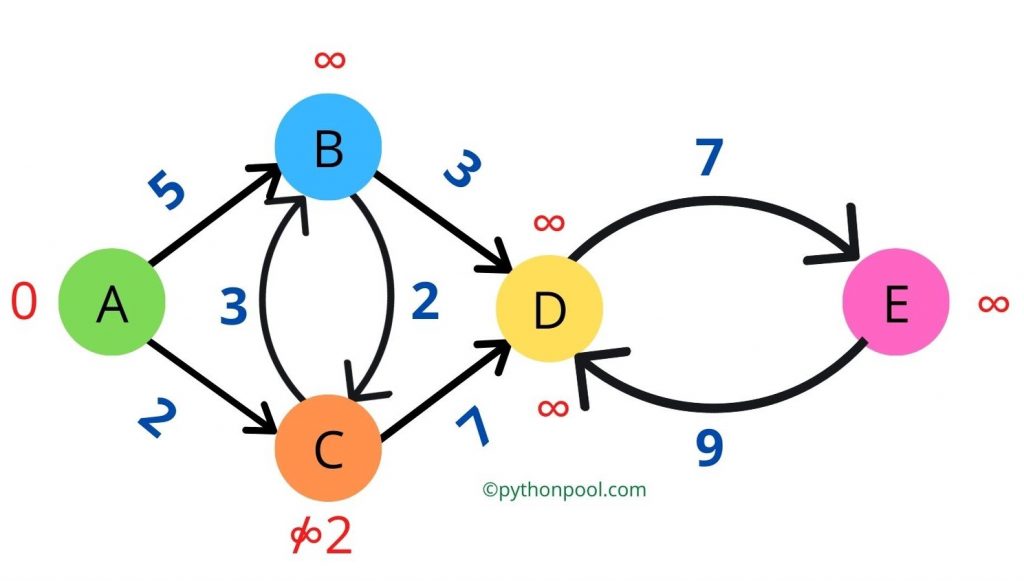
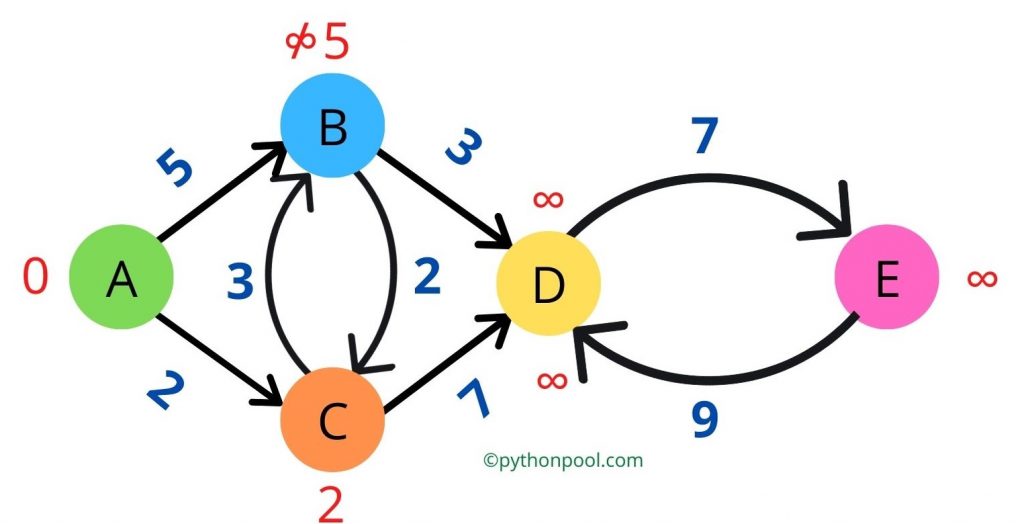
Step 4: After we have updated all the neighboring nodes of the current node’s values, it’s time to delete the current node from the unvisited_nodes.

From all those nodes that were neighbors of the current node, the neighbor chose the neighbor with the minimum_distance and set it as current_node. 

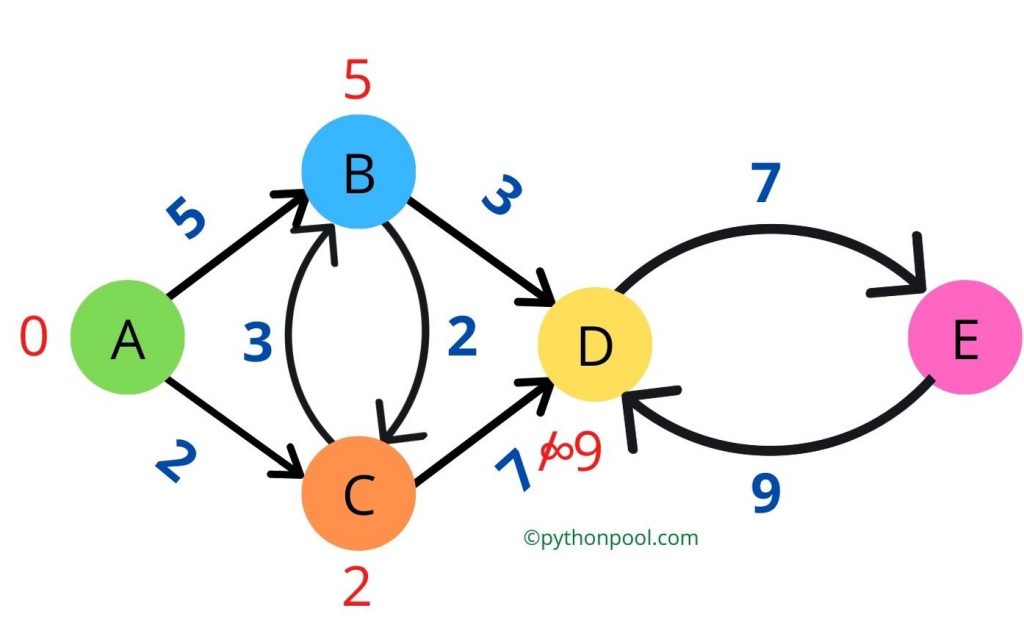
Step 5: Repeat steps 3 and 4 until and unless all the nodes in unvisited_visited nodes have been visited.  

Once all the nodes have been visited, we will get the shortest distance from the source node to the target node.  

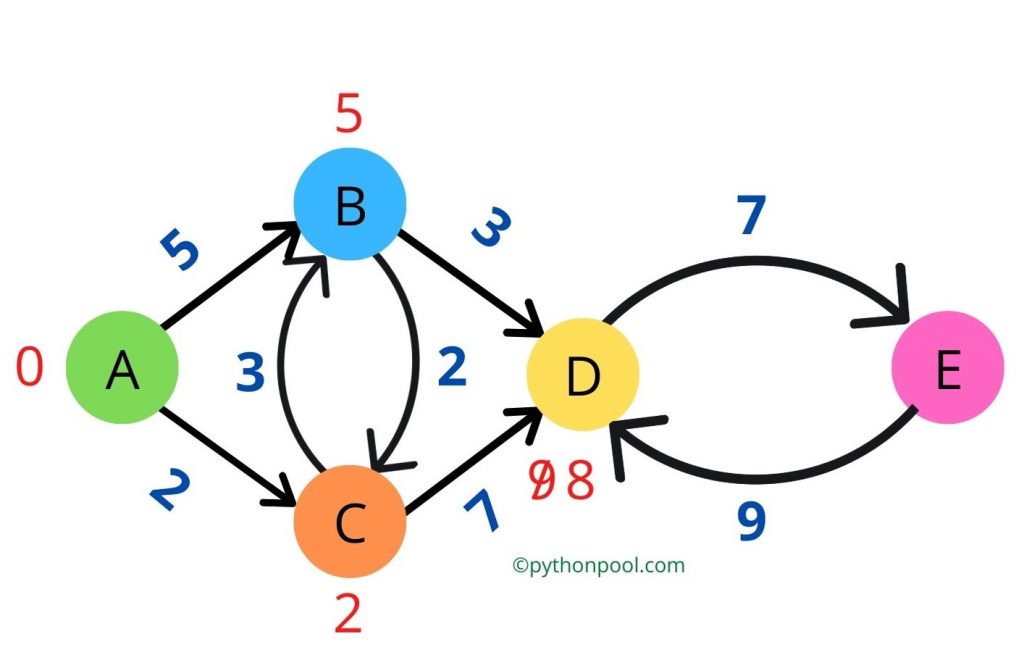
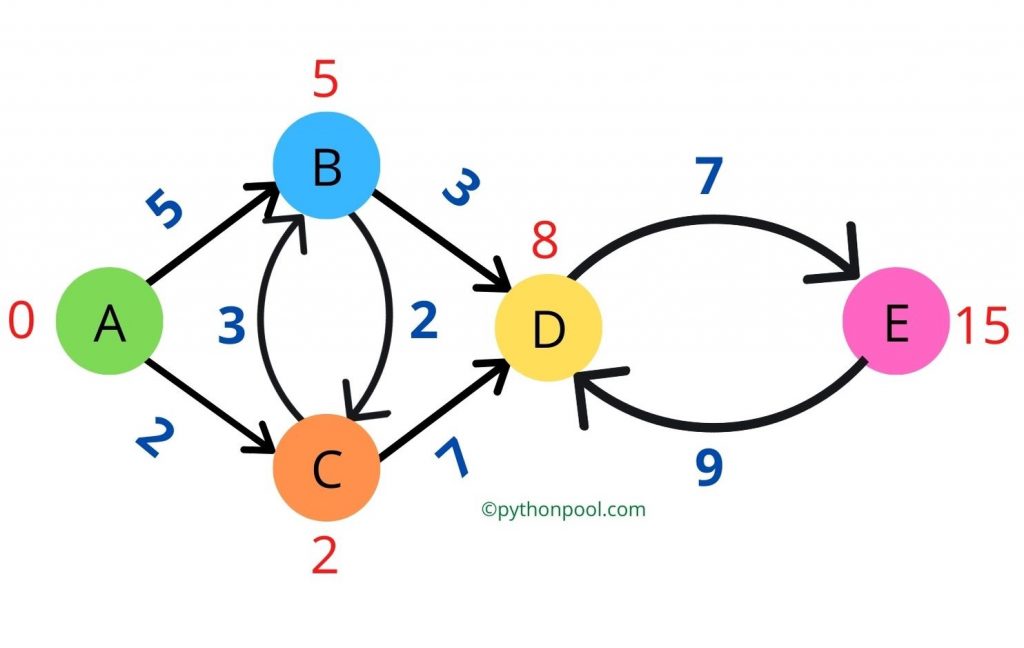
The output we got here is 15.

Now that we have the idea of how Dijkstra’s Algorithm works let us make a python program for it and verify our output from above.

Implementing Dijkstra’s Algorithm in Python 

def dijkstra(current, nodes, distances):
    # These are all the nodes which have not been visited yet
    unvisited = {node: None for node in nodes}
    # It will store the shortest distance from one node to another
    visited = {}
    # It will store the predecessors of the nodes
    currentDistance = 0
    unvisited[current] = currentDistance
    # Running the loop while all the nodes have been visited
    while True:
        # iterating through all the unvisited node
        for neighbour, distance in distances[current].items():
            # Iterating through the connected nodes of current_node (for 
            # example, a is connected with b and c having values 10 and 3
            # respectively) and the weight of the edges
            if neighbour not in unvisited: continue
            newDistance = currentDistance + distance
            if unvisited[neighbour] is None or unvisited[neighbour] > newDistance:
                unvisited[neighbour] = newDistance
        # Till now the shortest distance between the source node and target node 
        # has been found. Set the current node as the target node
        visited[current] = currentDistance
        del unvisited[current]
        if not unvisited: break
        candidates = [node for node in unvisited.items() if node[1]]
        print(sorted(candidates, key = lambda x: x[1]))
        current, currentDistance = sorted(candidates, key = lambda x: x[1])[0]
    return visited
 
nodes = ('A', 'B', 'C', 'D', 'E')
distances = {
    'A': {'B': 5, 'C': 2},
    'B': {'C': 2, 'D': 3},
    'C': {'B': 3, 'D': 7},
    'D': {'E': 7},
    'E': {'D': 9}}
current = 'A'
 
print(dijkstra(current, nodes, distances))

Output-

{'A': 0, 'C': 2, 'B': 5, 'D': 8, 'E': 15}

The answer is same that we got from the algorithm.

Must Read

• How to Convert String to Lowercase in
• How to Calculate Square Root
• User Input | Input () Function | Keyboard Input
• Best Book to Learn Python

Conclusion 

Dijkstra’s Algorithm in python comes very handily when we want to find the shortest distance between source and target. It can work for both directed and undirected graphs. The limitation of this Algorithm is that it may or may not give the correct result for negative numbers. In Google Maps, for finding the shortest route between one source to another, we use Dijkstra’s Algorithm. Another application is in networking, where it helps in sending a packet from source to destination.

Try to run the programs on your side and let us know if you have any queries.

Happy Coding!