Trees are a type of non – linear data structure. The trees are made up of nodes that are arranged in a hierarchical structure. It starts with a single root node which can have its own child nodes. All the nodes are connected with the help of edges. With trees, we can store information in a hierarchy. Depending on the number of children for each node, trees are classified into different types. In this article, we shall be performing Level Order Traversal in Python for trees.
What is traversal?
Traversing is the process of visiting each node of a tree, level by level, until all the nodes have been searched. Level order traversal is a traversing technique for breadth-first binary trees. Binary trees are trees where each node can have a maximum of two child nodes.
The traversing begins from the root node. Then, we progress towards the child nodes of the root node, then its child nodes, and so on until all the leaf nodes have been traversed. Using breadth-first traversal for a tree, we traverse the graph from the root node and gradually move towards its neighboring nodes. We check all the nodes present for a particular depth before moving to the next depth.
Let us understand the traversal with an example of the following tree.
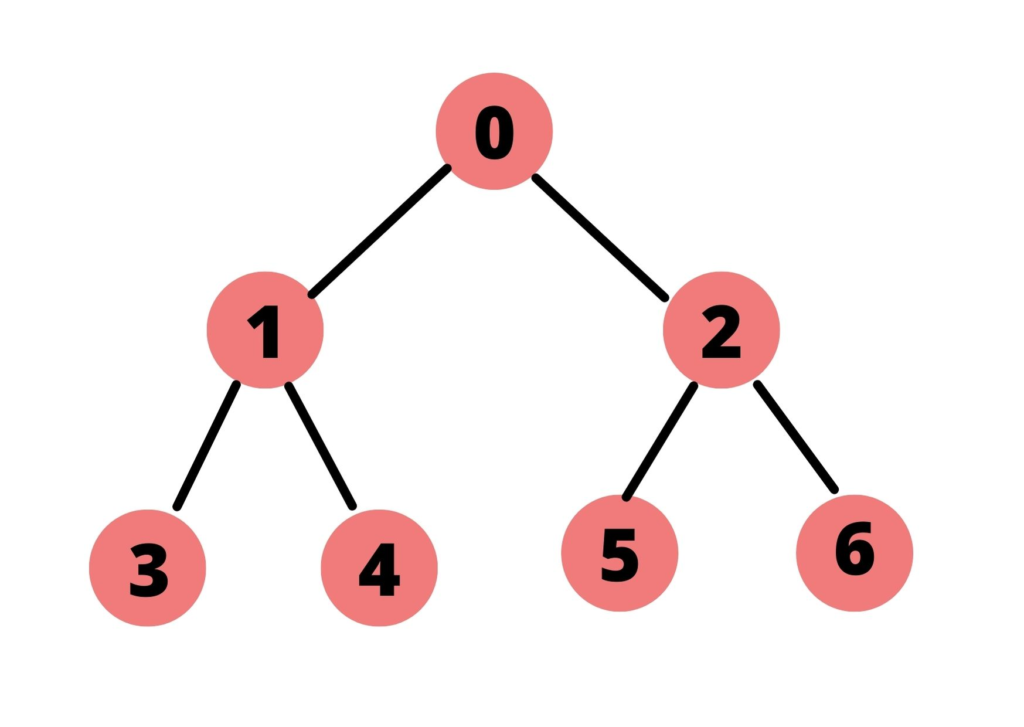
Here, node ‘0’ is the root node where node ‘1’ and node ‘2’ are its child nodes. Node ‘1’ is the left child node, and node ‘2’ being the right child node. Since it is a binary tree, each node can have a maximum of two child nodes. Then, node ‘3’ and node ‘4’ are child nodes of node ‘1’. Node ‘5’ and node ‘6’ are child nodes of node ‘2’.
If we were to perform a level order traversal of the above tree, it would be:
0 1 2 3 4 5 6
First, we would traverse the node ‘0’, then its child nodes – node ‘1’ and node ‘2’. After that, we would traverse the child nodes of node ‘1’ – node ‘3’ and node ‘4’. Then, at last, we would traverse the child nodes of node ‘2’ – node ‘5’ and node ‘6’. The traversal will stop after all the nodes have been traversed.
Implementing Level order Traversal in Python
We will implement the level order traversal in python using queues. The queue is a linear data structure. We store items inside a queue in a FIFO manner – First In, First Out. It simply means that the first element pushed inside the queue will also be the first element to be popped from the queue. We will implement queue using a list.
First, we will push the root node inside the queue. After the root nodes have been visited, we will pop out the root node and push its child nodes inside the queue.
For each child node, we shall traverse it and check if it has it is a root node to any other nodes. This shall continue until there are no more child nodes pushed into the queue and the queue becomes empty.
Python Code for Level Order Traversal
As mentioned above, we shall be performing level order traversal using a queue. We shall perform traversal for the following tree:
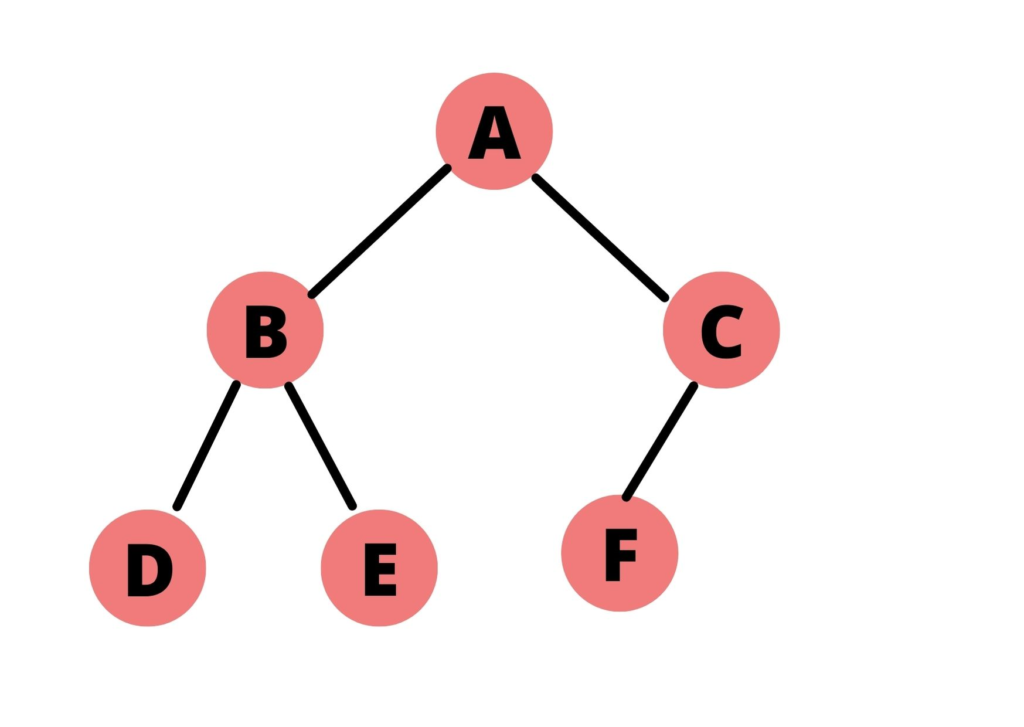
Here node ‘A’ is the root node. It has two child nodes – node ‘B’ is the left child node, and node ‘C’ is the right child node. Node ‘B’ has two child nodes – node ‘D,’ and node ‘E.’ Whereas node ‘C’ has only one child node – node ‘F.’
Defining the class
First, we shall define a class named ‘Tree’.
class Tree:
def __init__(self,node):
self.node = node
self.left = None
self.right = None
We will define the __init__() method, which will accept two arguments – self and node. We have initialized self.node to node. Initially, self.left and self.right will be None. The self.left and self.right represent the left and right child nodes respectively for the root node self.node.
Defining the function for traversal
Then, we shall define a function outside the class named ‘Level_Order_Traversal’.
def Level_Order_Traversal(root):
traversed = []
traversed.append(root)
if root is None:
return traversed
while traversed != []:
print(traversed[0].node)
x = traversed.pop(0)
if x.left:
traversed.append(x.left)
if x.right:
traversed.append(x.right)
The function accepts only one argument – ‘root’, which represents the root node. We have a list named ‘traversed’ which acts as a queue. First, we will append the list with the root which is actually a class object. Then, we shall check if our root is empty or not. If empty then we would return the empty queue ‘traversed’.
After that, we shall iterate a while loop which will run till the traversed list becomes empty. We shall print the root node using ‘print(traversed[0].node)’.
For the first element of the list, it will print its value. After that we shall pop the printed element from the list and save it into a variable named ‘x’. Then, we shall check if the node popped from the queue ‘traversed’ has any left child node.
If it has, then we shall append that left child node into ‘traversed’. Similarly, we shall also check for the right child node.
Creating class objects
First, we shall create the root ‘A’. Then using the left and right attributes, we shall create the entire tree. After that, we shall call the Level_Order_Traversal() function by passing root as an argument to it.
root = Tree('A')
root.left = Tree('B')
root.right = Tree('C')
root.left.left = Tree('D')
root.left.right = Tree('E')
root.right.left = Tree('F')
Level_Order_Traversal(root)
The output of the left order traversal is:
A B C D E F
The entire program is:
class Tree:
def __init__(self,node):
self.node = node
self.left = None
self.right = None
def Level_Order_Traversal(root):
traversed = []
traversed.append(root)
if root is None:
return traversed
while traversed != []:
print(traversed[0].node)
x = traversed.pop(0)
if x.left:
traversed.append(x.left)
if x.right:
traversed.append(x.right)
root = Tree('A')
root.left = Tree('B')
root.right = Tree('C')
root.left.left = Tree('D')
root.left.right = Tree('E')
root.right.left = Tree('F')
Level_Order_Traversal(root)
Execution of the code
Here, the first root node printed would be ‘A’ and popped from ‘traversed’. Then we would check if ‘A’ has any child nodes. So, ‘B’ and ‘C’ would be appended into ‘traversed’. The queue ‘traversed’ would be:
Traversed : |A| B | C | | | |
Then, we would print the node ‘B’ and pop it from the queue. After that, we would check if node ‘B’ has any left child nodes or right child nodes. Since it does have child nodes, ‘D’ and ‘E’ would be appended into ‘traversed’.
Traversed : |A|B| C | D | E | |
After that, we shall print node ‘C’ and pop it from the queue. Then, we will check if it has any child nodes. Since it has one left child node – ‘F’, we would append that into ‘traversed’.
Traversed : |A|B|C| D | E | F |
Now, we shall print ‘D’ and pop it from the queue. Since ‘D’ has no child nodes, we will not append anything to the queue. Similarly, we will print ‘E’ and ‘F’ one by one and pop them from the queue.
Traversed : |A|B|C|D|E|F|
Since the queue ‘traversed’ is empty now, the while loop will stop its execution.
This sums up the left order traversal in python. If you have any questions in your mind, feel free to leave them in the comments below.
Until next time, Keep Learning!