Softmax Function Using Numpy in Python

Here we are going to learn about the softmax function using the NumPy library in Python. We can implement a softmax function in many frameworks of Python like TensorFlow, scipy, and Pytorch. But, here, we are going to implement it in the NumPy library because we know that NumPy is one of the efficient and powerful libraries.

Softmax is commonly used as an activation function for multi-class classification problems. Multi-class classification problems have a range of values. We need to find the probability of their occurrence.

What is softmax function?

Softmax is a mathematical function that takes a vector of numbers as an input. It normalizes an input to a probability distribution. The probability for value is proportional to the relative scale of value in the vector.

Before applying the function, the vector elements can be in the range of (-∞, ∞). After applying the function, the value will be in the range of [0,1]. The values will sum up to one so that they can be interpreted as probabilities.

The softmax function formula is given below.

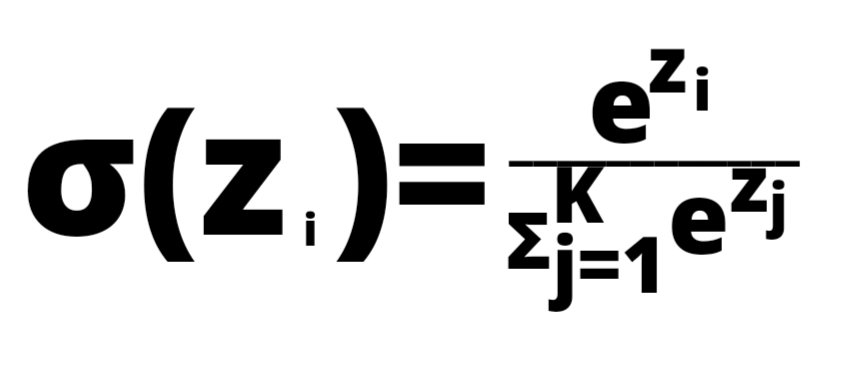
How does softmax function work using numpy?

If one of the inputs is large, then it turns into a large probability, and if the input is small or negative, then it turns it into a small probability, but it will always remain between the range that is [0,1]

Benefits of softmax function

• Softmax classifiers give probability class labels for each while hinge loss gives the margin.
• It’s much easier to interpret probabilities rather than margin scores (such as in hinge loss and squared hinge loss).

Examples to Demonstrate Softmax Function Using Numpy

If we take an input of [0.5,1.0,3.0] the softmax of that is 
[0.02484727, 0.04096623, 0.11135776]

Let us run the example in the python compiler.

>>> import numpy as np
>>> a=[0.5,1.0,2.0]
>>> np.exp(a)/np.sum(np.exp(a))

The output of the above example is

array([0.02484727, 0.04096623, 0.11135776])

Implementing Softmax function in Python

Now we are well about the softmax formula. Here are going to use the NumPy sum() method to calculate our denominator sum and the NumPy exp() method for calculating the exponential of our vector.

import numpy as np
vector=np.array([6.0,3.0])
exp=np.exp(vector)
probability=exp/np.sum(exp)
print("Probability distribution is:",probability)

First, we are importing a NumPy library as np. Secondly, creating a variable named vector. A variable vector holds an array. Thirdly implementing the formula to get the probability distribution.

Output

Probability distribution is: [0.95257413 0.04742587]

Softmax Cross Entropy Using Numpy

Using the softmax cross-entropy function, we would measure the difference between the predictions, i.e., the network’s outputs.

Code

import numpy as np
import matplotlib.pyplot as plt
def sig(x):
    return 1.0/(1.0+np.exp(-x))
def softmax_cross_entropy(z,y):
    if y==1:
        return -np.log(z)
    else:
        return -np.log(1-z)
x=np.arange(-9,9,0.1)
a=sig(x)
softmax1=softmax_cross_entropy(a,1)
softmax2=softmax_cross_entropy(a,0)
figure,axis=plt.subplots(figsize=(7,7))
plt.plot(a,softmax1)
plt.plot(a,softmax2)
plt.xlabel("Cross entropy loss")
plt.ylabel("log loss")
plt.show()

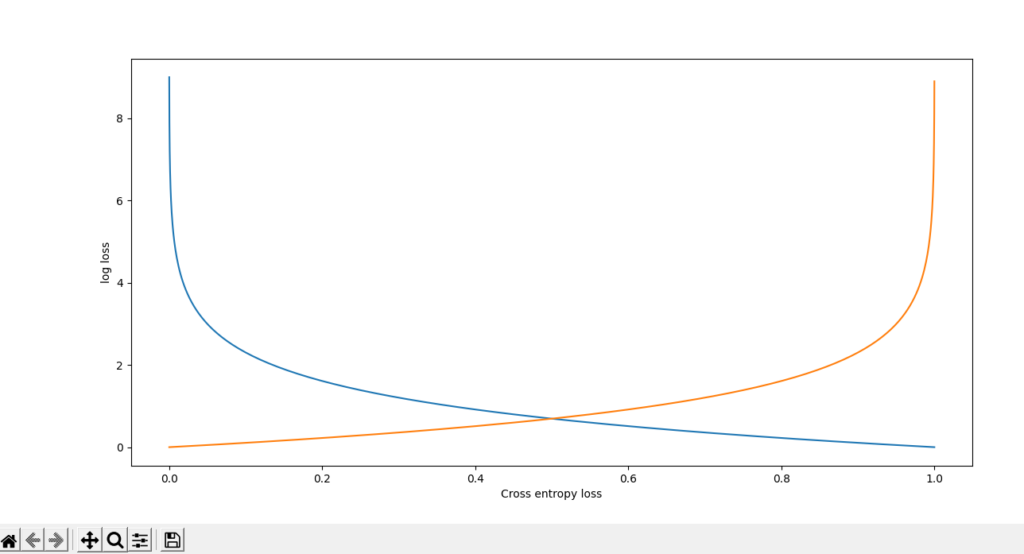
First, importing a Numpy library and plotting a graph, we are importing a matplotlib library. Next creating a function names “sig” for hypothesis function/sigmoid function. Creating another function named “softmax_cross_entropy” . z represents the predicted value, and y represents the actual value. Next, calculating the sample value for x. And then calculating the probability value. Value of softmax function when y=1 is -log(z) and when y=0 is -log(1-z). So now going to plot the graph. Giving x-label and y-label. plt.show() is used to plot the graph.

Here is the graph is shown for cross-entropy loss/log loss.

Output

Frequently asked questions related to the numpy softmax function

Conclusion

Here we have seen about softmax using Numpy in Python. Softmax is a mathematical function. We can implement the softmax function in many frameworks like Pytorch, Numpy, Tensorflow, and Scipy.