Python Vector, in layman’s language, is nothing but a one-dimensional array of numbers. The only difference between python vectors and arrays is that. Unlike typical arrays, the vectors’ data, and size are mutable. The vectors are also known as dynamic arrays. Arrays and vectors are both basic data structures. The Vectors in Python comprising of numerous values in an organized manner.
Python Vectors can be represented as: v = [v1, v2, v3].
Here v is a single-dimensional array having v1, v2, and v3 as ordinary numeral values.
Python Vector operations using NumPy library:
Single dimensional arrays are created in python by importing an array module. The multi-dimensional arrays cannot be created with the array module implementation. Vectors are created using the import array class. However, various operations are performed over vectors. Some of the operations include basic addition, subtraction, multiplication, division. Some other operations include dot product and cross product of two vectors.
You can also do operations on those who are not available in the array module. So, to implement multidimensional arrays ( single-dimensional arrays can also be created). For doing the faster operations on arrays and vectors, one such library containing all such functions is NumPy. For instance, the NumPy module is thus imported into the python program for the required vectors’ operations.
Importing NumPy for Python Vector:
If we write import NumPy in our programs while using any python 3 versions. It shows an error. The NumPy package is not available by default. We need to install it manually. Python has an amazing tool called the pip (pip install packages). Moreover, the pip package has many such packages that are not present in python by default. You can install a lot of packages using the pip. Pip can be used to install the Numpy package and to run the python program error-free.
Vector definition in python:
We can define a vector in python as a NumPy array. For example:
#create a vector
from numpy import array
vec = array([1, 5, 6])
print(vec)
This example defines a vector of three elements and print them as:
[1, 5, 6]
Addition of vectors in Python:
# addition of vectors
from numpy import array
x = array([1, 5, 6])
print(x)
y = array([1, 5, 6])
print(y)
z = x + y
print(z)
The output of the above python code for addition of two numbers is :
[1, 5, 6]
[1, 5, 6]
[2, 10, 12]
Explanation:
Fistly, the final vector’s length is the same as the two parents’ vectors. Each element of the new vector is the sum of the two vectors. NumPy allows compact and direct addition of two vectors. Without using the NumPy array, the code becomes hectic. Also, it would require the addition of each element individually. And then creating a new vector to store them. The other basic arithmetic operations like subtraction, multiplication, and division. Similarly, using the NumPy package these operations can be done in a similar way. Just the operator changes depending upon the operation.
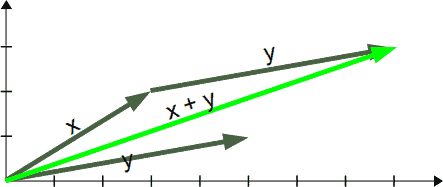
Subtraction of vectors in Python:
# addition of vectors
from numpy import array
x = array([1, 5, 6])
print(x)
y = array([1, 4, 6])
print(y)
z = x - y
print(z)
The output of the above python code for subtraction of two numbers is :
[1 5 6]
[1 4 6]
[0 1 0]
Explanation:
We start by importing the Numpy module and initializing two arrays. Both of these arrays are three dimensional and have different reference points. You can easily subtract these two arrays using the ‘-‘ operator. In addition operation, the minus operator also performs in the same way.
Python Vector Dot Product:
#vector dot product
from numpy import array
x = array([1, 2, 3])
print(x)
y = array([1, 2, 5])
print(y)
z = x.dot(y)
print(z)
The output of the dot product of the above two vectors is:
[1, 2, 3]
[1, 2, 5]
20
Explanation:
Dot product calculates the sum of the two vectors’ multiplied elements. Dot Product returns a scalar number as a result. The dot product is useful in calculating the projection of vectors. Dot product in Python also determines orthogonality and vector decompositions. The dot product is calculated using the dot function, due to the numpy package, i.e., .dot().
Python Vector Cross Product:
Python Vector Cross product works in the same way as the normal cross product. A cross vector is defined as a vector that is perpendicular to these two vectors with a magnitude equal to the area of the parallelogram spanned by both vectors. As of now, the vector object honest has a cross multiplication method like that of a dot. We’ll have to use np.cross() to find the cross product.
#vector cross product
from numpy import array
import numpy as np
x = array([1, 2, 3])
print(x)
y = array([1, 2, 5])
print(y)
z = np.cross(x, y)
print(z)
The output of the dot product of the above two vectors is:
[1 2 3]
[1 2 5]
[ 4 -2 0]
Explanation:
Cross Product returns a vector that is perpendicular to both vectors. Firstly, we start by importing the numpy module and array class from it. Nextly, we initialize two arrays with different values. As a cross product of the same vector gives a zero vector, we have to use two different vectors. At last, np.cross() returns the cross multiplied vector of two NumPy arrays.
Multiplication of a Python Vector with a scalar:
# scalar vector multiplication
from numpy import array
a = array([1, 2, 3])
print(a)
b = 2.0
print(s)
c = s * a
print(c)
The output of the above vector scalar multiplication in python is :
[1, 2, 3]
2.0
[2.0, 4.0, 6.0]
Explanation:
Vector scalar multiplication in python is a straightforward thing to understand. It is just the multiplication of all the vectors’ elements. Ordinary numbers are used for the multiplication of vector elements, i.e., a scalar. The returning that multiplied vector as the new vector output.
Unit Vector of Python Vector:
Unit Vectors are the vectors with the same directions as a normal vector but their magnitude equals 1. These vectors are amazingly important for carrying out multiple operations in 3d space. As there is no available method to convert the vector into normal form, we’ll have to use the sum() method of the numpy array.
#unit vector product
from numpy import array
x = array([1, 2, 3])
x_hat = x / (x**2).sum()**0.5
print(x)
The output of the above vector scalar multiplication in python is :
[0.26726124 0.53452248 0.80178373]
Explanation:
Firstly, we import the necessary classes and initialize a dummy array x. This array has a magnitude not equal to 1. To convert it to 1, we first find its magnitude and divide it. (x**2).sum()**0.5 is used to find the magnitude of vector x.
Must Read
- Introduction to Python Super With Examples
- Python Help Function
- Why is Python sys.exit better than other exit functions?
- Python Bitstring: Classes and Other Examples | Module
Conclusion:
Python vector is simply a one-dimensional array. We can perform all operations using lists or importing an array module. But installing and importing the NumPy package made all the vector operations easier and faster. Vectors are plotted and drawn using arrows by importing matplotlib.pyplot. To draw vectors with arrows in python, the function used is matplotlib.pyplot.quiver(). However, the quiver function takes four arguments. Out of which, the first two arguments are the data about where the arrows will be. And the other two take the data of the ending point of the arrows.
Still have any doubts or questions do let me know in the comment section below. I will try to help you as soon as possible.
Happy Pythoning!
