A* Algorithm in Python or in general is basically an artificial intelligence problem used for the pathfinding (from point A to point B) and the Graph traversals. This algorithm is flexible and can be used in a wide range of contexts. The A* search algorithm uses the heuristic path cost, the starting point’s cost, and the ending point. This algorithm was first published by Peter Hart, Nils Nilsson, and Bertram Raphael in 1968.
Why A* Algorithm?
This Algorithm is the advanced form of the BFS algorithm (Breadth-first search), which searches for the shorter path first than, the longer paths. It is a complete as well as an optimal solution for solving path and grid problems.
Optimal – find the least cost from the starting point to the ending point. Complete – It means that it will find all the available paths from start to end.
Basic concepts of A*
Where
g (n) : The actual cost path from the start node to the current node.
h ( n) : The actual cost path from the current node to goal node.
f (n) : The actual cost path from the start node to the goal node.
For the implementation of A* algorithm we have to use two arrays namely OPEN and CLOSE.
OPEN:
An array that contains the nodes that have been generated but have not been yet examined till yet.
CLOSE:
An array which contains the nodes which are examined.
Algorithm
1: Firstly, Place the starting node into OPEN and find its f (n) value.
2: Then remove the node from OPEN, having the smallest f (n) value. If it is a goal node, then stop and return to success.
3: Else remove the node from OPEN, and find all its successors.
4: Find the f (n) value of all the successors, place them into OPEN, and place the removed node into CLOSE.
5: Goto Step-2.
6: Exit.
Advantages of A* Algorithm in Python
- It is fully complete and optimal.
- This is the best one of all the other techniques. We use to solve all the complex problems through this algorithm.
- The algorithm is optimally efficient, i.e., there is no other optimal algorithm that is guaranteed to expand fewer nodes than A*.
Disadvantages of A* Algorithm in Python
- This algorithm is complete if the branching factor is finite of the algorithm and every action has a fixed cost.
- The speed execution of A* search is highly dependant on the accuracy of the heuristic algorithm that is used to compute h (n) and is a bit slower than other algorithms.
- It is having complex problems.
Pseudo-code of A* algorithm
let openList equal empty list of nodes
let closedList equal empty list of nodes
put startNode on the openList (leave it's f at zero)
while openList is not empty
let currentNode equal the node with the least f value
remove currentNode from the openList
add currentNode to the closedList
if currentNode is the goal
You've found the exit!
let children of the currentNode equal the adjacent nodes
for each child in the children
if child is in the closedList
continue to beginning of for loop
child.g = currentNode.g + distance b/w child and current
child.h = distance from child to end
child.f = child.g + child.h
if child.position is in the openList's nodes positions
if child.g is higher than the openList node's g
continue to beginning of for loop
add the child to the openListA* Algorithm code for Graph
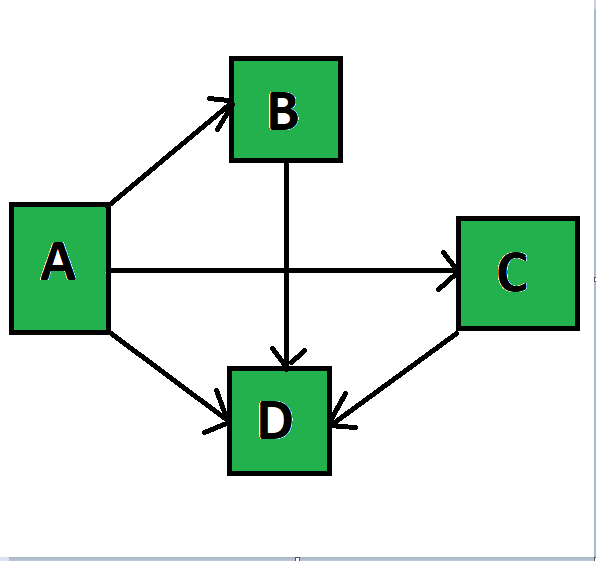
A* algorithm is best when it comes to finding paths from one place to another. It always makes sure that the founded path is the most efficient. This is the implementation of A* on a graph structure
from collections import deque
class Graph:
def __init__(self, adjac_lis):
self.adjac_lis = adjac_lis
def get_neighbors(self, v):
return self.adjac_lis[v]
# This is heuristic function which is having equal values for all nodes
def h(self, n):
H = {
'A': 1,
'B': 1,
'C': 1,
'D': 1
}
return H[n]
def a_star_algorithm(self, start, stop):
# In this open_lst is a lisy of nodes which have been visited, but who's
# neighbours haven't all been always inspected, It starts off with the start
#node
# And closed_lst is a list of nodes which have been visited
# and who's neighbors have been always inspected
open_lst = set([start])
closed_lst = set([])
# poo has present distances from start to all other nodes
# the default value is +infinity
poo = {}
poo[start] = 0
# par contains an adjac mapping of all nodes
par = {}
par[start] = start
while len(open_lst) > 0:
n = None
# it will find a node with the lowest value of f() -
for v in open_lst:
if n == None or poo[v] + self.h(v) < poo[n] + self.h(n):
n = v;
if n == None:
print('Path does not exist!')
return None
# if the current node is the stop
# then we start again from start
if n == stop:
reconst_path = []
while par[n] != n:
reconst_path.append(n)
n = par[n]
reconst_path.append(start)
reconst_path.reverse()
print('Path found: {}'.format(reconst_path))
return reconst_path
# for all the neighbors of the current node do
for (m, weight) in self.get_neighbors(n):
# if the current node is not presentin both open_lst and closed_lst
# add it to open_lst and note n as it's par
if m not in open_lst and m not in closed_lst:
open_lst.add(m)
par[m] = n
poo[m] = poo[n] + weight
# otherwise, check if it's quicker to first visit n, then m
# and if it is, update par data and poo data
# and if the node was in the closed_lst, move it to open_lst
else:
if poo[m] > poo[n] + weight:
poo[m] = poo[n] + weight
par[m] = n
if m in closed_lst:
closed_lst.remove(m)
open_lst.add(m)
# remove n from the open_lst, and add it to closed_lst
# because all of his neighbors were inspected
open_lst.remove(n)
closed_lst.add(n)
print('Path does not exist!')
return None
INPUT:
adjac_lis = {
'A': [('B', 1), ('C', 3), ('D', 7)],
'B': [('D', 5)],
'C': [('D', 12)]
}
graph1 = Graph(adjac_lis)
graph1.a_star_algorithm('A', 'D')
OUTPUT:
Path found: ['A', 'B', 'D']
['A', 'B', 'D']Explanation:
In this code, we have made the class named Graph, where multiple functions perform different operations. There is written with all the functions what all operations that function is performing. Then some conditional statements will perform the required operations to get the minimum path for traversal from one node to another node. Finally, we will get the output as the shortest path to travel from one node to another.
Also, Read
Conclusion
A* in Python is a powerful and beneficial algorithm with all the potential. However, it is only as good as its heuristic function, which is highly variable considering a problem’s nature. It has found its applications in software systems in machine learning and search optimization to game development.

great