Today we will discuss the main algorithm, which has many implementations in real life, i.e., breadth-first search using python. Till now, you must be curious enough to know how this algorithm is related to the BFS algorithm. So, without doing any delay, let’s start our today’s tutorial on BFS.
You must have used google maps to go from one destination to another using the shortest route or solved Rubik’s cube. These are the real-life scenarios that use the BFS algorithm, or you might say that these real-life examples are part of the implementation of BFS.
Overview on BFS
Breadth-first search (BFS) in python is an algorithm that does tree traversal on graphs or tree data structures. BFS implementation uses recursion and data structures like dictionaries and lists in python.
Breadth-first search starts by searching a start node, followed by its adjacent nodes, then all nodes that can be reached by a path from the start node containing two edges, three edges, and so on.
Formally, the BFS algorithm visits all vertices in a graph G that are k edges far away from the source vertex s before visiting any vertex (k+1) edges away. This is done until there are no more vertices left that are reachable from s.
Let us consider the following diagram. This is a BFS
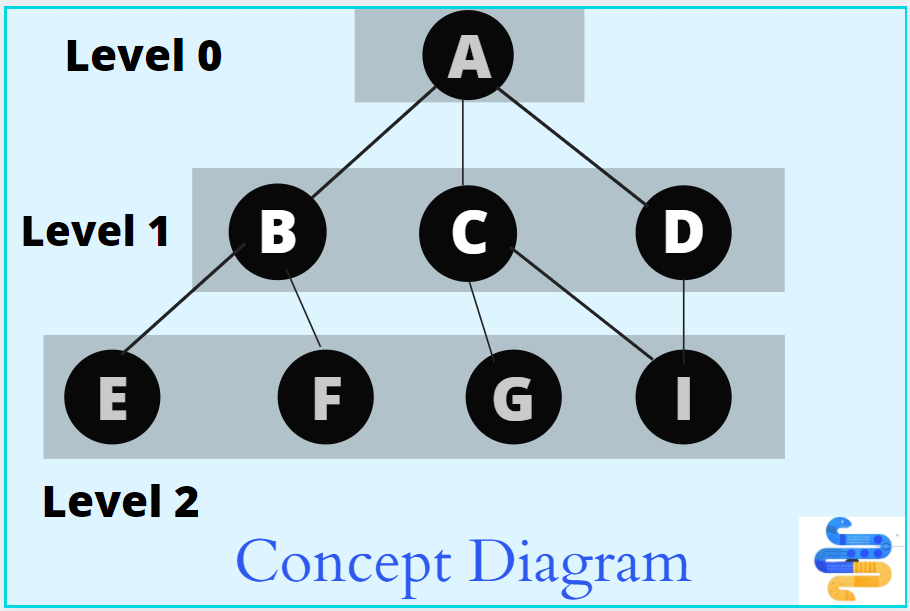
From the above diagram of graph G, we can say that A, B, C, D, E, F, G, H are the nodes. A is the source vertex. B, C, D are the edges that can be reached through the source vertex A.
How to traverse in BFS using python?
There are specific rules in which we traverse.
As in the example given above, the BFS algorithm traverses from A to B to D to E first, then B to C, then E to F, and lastly, F to G and H. It employs the following rules.
- Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
- Rule 2 − If no adjacent vertex is found, then remove the first vertex from the queue.
- Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.
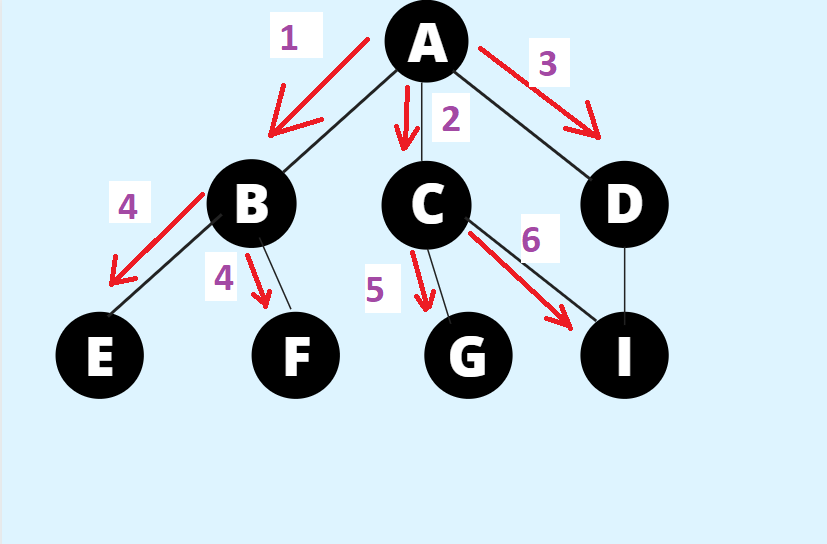
From the above graph G, performing a breadth-first search and then determining the source node, the list of visited nodes (V), and the state of the queue (Q) at each step.
- At level 0, the root node is A.
- Similarly, at level 1, the root node is B, C, D
- Finally, at level 2, the node is E, F, G, I.
As you can see the way it arrives.
Rules of the BFS algorithm using python
Here, are important rules for using BFS algorithm:
- A queue is a FIFO data structure, i.e., First-in First-Out, that should be used by BFS.
- You mark any node in the graph as root and start traversing the data from it:- As in our case, the starting root is A.
- The BFS algorithm will traverse all the nodes in the graph starting from the root and keep them dropping after they are completed or visited:- In our case, A node is visited, then it was dropped from the queue.
- BFS visits an adjacent unvisited node, marks it as done, and inserts it into a queue.
- Remove the previous vertex from the queue if in case there is no adjacent vertex.
- BFS algorithm will iterate until all the vertices are traversed.
- If completely traversed, then it will mark them as completed.
Pseudo Code of BFS in Python
BFS (visits, graph, node) // visits is the visited nodes, graph is the graph and node is the source node or the root
let Q be queue.
Q.enqueue(node) // Adding node to queue to find its neighbors
mark node as visited.
while Q is not empty:
v = Q.dequeue() // removing the front item in queue
for neighbours w of v in Graph graph // get all the neighbours of v and add them to queue
if w is not visited
Q.enqueue(w) // add to Q for next search
mark w as visitedNow we have understood the concept very well. So lets start coding it in python.
graph = {
'A': ['B', 'C', "D"],
'B': ['E', "F"],
'C': ['G', "I"],
'D': ["I"],
'E': [],
"F": [],
'G': [],
"I": []
}
def bfs(visit_complete, graph, current_node):
visit_complete.append(current_node)
queue = []
queue.append(current_node)
while queue:
s = queue.pop(0)
print(s)
for neighbour in graph[s]:
if neighbour not in visit_complete:
visit_complete.append(neighbour)
queue.append(neighbour)
bfs([], graph, 'A')
OUTPUT:-
A B C D E F G I
Explanation of the code
- Created the graph using a dictionary.
- Declared the list called visited to keep track of the visited nodes.
- Declared a list called queue so that we can keep track of its edges.
- Then, declaring a function called bfs and passing the parameters as visited, graph and node.
- As we are traversing, the node we are adding to the visited list.
- We are keeping track of its edges and adding them into the queue.
- We are removing the visited node by poping it.
- Then, we are printing the node already visited.
- Now, we are moving to the edges if there are no adjacent nodes left.
- We are performing the same operation of popping once we visited the node.
Time Complexity of BFS in Python
The time complexity of BFS is O(V + E), where V is the number of nodes and E is the number of edges.
Must Read
FAQs
1. Why do we prefer queues instead of other data structures while implementing BFS?
- BFS searches for nodes level-wise, i.e., starting from level 0, it searches the nodes w.r.t their distance from the root (or source).
- From the above example, we saw that BFS required us to visit the child nodes discovered by their parents.
- Whenever we visit a node, we insert all the neighboring nodes into our data structure. Therefore, if a queue data structure is used, it will guarantee that we get the nodes in order their parents was found as the queue follows the FIFO (first in, first out) flow.
2. Is BFS a complete algorithm?
- A search algorithm is said to be complete. If at least one solution exists, then the algorithm is guaranteed to find a solution in a finite amount of time. Thus, BFS is complete.
3. Is BFS a optimal algorithm?
- A search algorithm is optimal if it finds a solution. Moreover, it finds that in the best possible manner. Thus, BFS is optimal, so it is being used in cases to find a single answer optimally.
4. Difference between BFS and DFS in Python?
| BFS | DFS |
| BFS stands for Breadth-First Search. | DFS stands for Depth-First Search. |
| It is a vertex-based technique. | It is an edge-based technique. |
| BFS uses a Queue data structure that follows first in, first out. | BFS uses the Stack data structure that follows Last in first out. |
| In BFS, one vertex is selected at a time when it is visited and marked. Then its adjacent are visited and stored in the queue. | It is performed in two stages, first visited vertices are pushed into the stack and second, if there are no vertices, then visited vertices are popped. |
| BFS is a bit slower process as compared to DFS. | DFS is faster than BFS. |
Conclusion
We have discussed the python implementation of BFS in detail. We can also understand the importance of BFS as it has many applications in real life. Hope the concepts are clear.
Keep reading our articles folks. Till then keep Pythoning.
