Data Structures are ways of arranging or storing different types of data efficiently. They are an essential part of many different algorithms and allow us, programmers, to efficiently maintain the data. We look for a way to store our data such that it requires minimum memory storage consumption,.And the time taken to retrieve the data from it should be minimal. One such important data structure is python max heap.
A max heap is a special kind of tree (must be a complete binary tree), where we store data in such a way that every parent node is greater than or equal to each of its child nodes. It means that the parent of each complete tree should be the largest number in that tree. In this article, we will try to cover everything about max heap from the very basics.
What is Max Heap in Python, and Why is it used?
We now know that in a max heap, all the items are ordered such that the child nodes are smaller in value than their parent node. It can be represented (or arranged) in the form of an array where the first element is the largest. And if all the items are in such a way that the child is smaller than or equal to its parent, then this type of arrangement is known as min-heap.
Importance of Python Min Heap
In Software Engineering Interviews, a lot of questions are asked on these heaps. The reason behind it is that heaps are very useful in the implementation of priority queues. And priority queues are significant in Operating Systems for prioritizing the tasks. By prioritizing the tasks, it means what tasks the operating system should focus on first and what job it should not focus on at first. It is because of the limitation of the availability of resources in a multi-tasking system. It is significant for the operating system to decide how to allocate resources to all tasks such that every job gets completed in the order of importance. In short, the priority queue is useful for load balancing.
Must Read | Min Heap In Python And Its Operations
Representation of a Python Max Heap
A max heap is generally represented using an array (or a python list) where the first element is the largest in that array.
Let suppose we have a max heap-
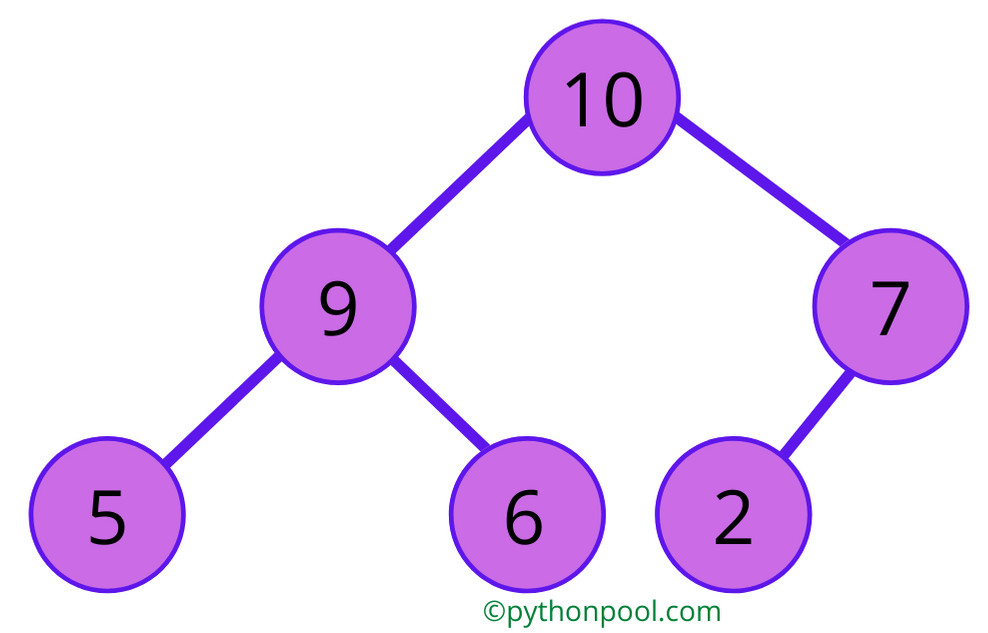
It can be represented in array as-[10 ,9 ,7 ,5 ,6 ,2 ]
We can see that the elements are arranged in such a manner that every child is smaller in value than its parent.
One more important thing we should know that is that the parent of the child is at index-
Arr[(i-1)/2]
Where Arr is the array- [10, 9, 7 ,5 ,6, 2]
‘i’ is the index of the child.
So, For example, the parent node for element=5 (index=3) is-
Arr[(3-1)/2] = Arr[2/2)] = Arr[1] = 9
Note- Here, the index starts from ‘0’.
Similarly, if we want to find the children of a particular parent node, the formula is:
Left Child = Arr[2*i+ 1]
Where i= index of a parent node.
Suppose, we want to find the left child of 10 (index=0)
Arr[2*0+1] = Arr[1] = 9
Right Child = Arr[2*i+2]
Suppose, we want to find the right child of element ‘9’ (index=1)
Arr[(2*1)+1] = Arr[2+1] = Arr[3] = 5
We have covered almost everything important in theoretical part about the max heap and it’s time for us to jump directly to the implementation part.
Implementing Max Heap in Python
Operations:
- push() – We can insert every element to the heap. We always add the item at the end of the tree. The time complexity of the operation is O(log(n)). Every time we make an insertion, we have to ensure that the heap is still in the correct order by checking the value of the new element with the parent.
- Pop ()– We can delete the root of the heap. We have to swap the root with the last item and again check whether the heap is still in order. And if not, we have to make it as a heap. The time complexity of this operation is also O(log(n)).
- Peek () – Using peek, we can look at the heap’s first value (largest value). The time complexity of the peek operation is O(1).
Program of Max Heap in Python
class Max_Heap:
# initializing the constructor with arr (array that we have to convert into heap). The default value is None([])
def __init__(self, arr=[]):
# Initializing the heap with no elements in it
self._heap = []
# If the array by the user is not empty, push all the elements
if arr is not None:
for root in arr:
self.push(root)
# push is used to insert new value to the heap
def push(self, value):
# Appending the value given by user at the last
self._heap.append(value)
# Calling the bottom_up() to ensure heap is in order.
# here we are passing our heap
_bottom_up(self._heap, len(self) - 1)
# push is used to insert new value to the heap
def pop(self):
if len(self._heap)!=0:
# swapping the root value with the last value.
_swap(self._heap, len(self) - 1, 0)
# storing the popped value in the root variable
root = self._heap.pop()
#Calling the top_down function to ensure that the heap is still in order
_top_down(self._heap, 0)
else:
root="Heap is empty"
return root
# It tells the length of the heap
def __len__(self):
return len(self._heap)
# print the first element (The root)
def peek(self):
if len(self._heap)!=0:
return(self._heap[0])
else:
return("heap is empty")
# Swaps value in heap between i and j index
def _swap(L, i, j):
L[i], L[j] = L[j], L[i]
# This is a private function used for traversing up the tree and ensuring that heap is in order
def _bottom_up(heap, index):
# Finding the root of the element
root_index = (index - 1) // 2
# If we are already at the root node return nothing
if root_index < 0:
return
# If the current node is greater than the root node, swap them
if heap[index] > heap[root_index]:
_swap(heap, index,root_index)
# Again call bottom_up to ensure the heap is in order
_bottom_up(heap, root_index)
# This is a private function which ensures heap is in order after root is popped
def _top_down(heap, index):
child_index = 2 * index + 1
# If we are at the end of the heap, return nothing
if child_index >= len(heap):
return
# For two children swap with the larger one
if child_index + 1 < len(heap) and heap[child_index] < heap[child_index + 1]:
child_index += 1
# If the child node is smaller than the current node, swap them
if heap[child_index] > heap[index]:
_swap(heap, child_index, index)
_top_down(heap, child_index)
# Making the object of the Heap class and passing the array to convert into heap
m=Max_Heap([1,2,3,4,5,6])
# Checking the value at top
print("Value at top:",m.peek())
# pushing elements into heap
m.push(1)
m.push(11)
print("Value at top:",m.peek())
# Deleting the root node
print("Root popped:",m.pop())
m.push(7)
m.push(9)
m.push(15)
print("Value at top:",m.peek())
print("Root popped:",m.pop())
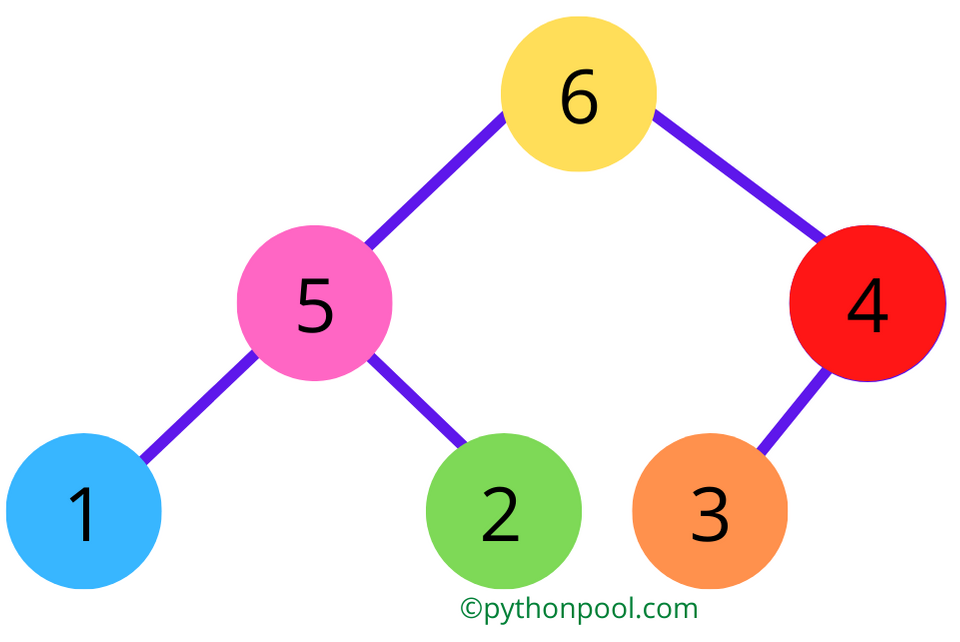
Output-
Value at top: 6 Value at top: 11 Root popped: 11 Value at top: 15 Root popped: 15
The resultant heap is-
Must Read
- How to Convert String to Lowercase in
- How to Calculate Square Root
- User Input | Input () Function | Keyboard Input
- Best Book to Learn Python
Conclusion
We have learned the implementation of the max heap in python from scratch because to understand the working behind any data structure we must know the working behind it. In Operating Systems the use of heap sort using heap to allocate the resources to tasks with higher weightage is given more priority while processing.
Try to run the programs on your side and let us know if you have any queries.
Happy Coding!
