Scipy fsolve Is Useful To Solve A Non-Linear Equations

In this article, we will see how to solve a non-linear equation in python. In python, there are a lot of methods available to solve non-linear equations. Here we are using scipy.fsolve to solve a non-linear equation. There are two types of equations available, Linear and Non-linear. An equation is an equality of two expressions.

A Non-linear equation is a type of equation. The degree in non-linear equations is two or more than two. The general equation of a linear equation is Ax+ By+ C=0 is a linear equation. Other than that are a non-linear equation. The general equation is :

Ax2 + By2 = C

Where A, B, and C are constants, x and y are variables. It forms a curve when it is plotted on a graph.

What is fsolve?

It is a function in a scipy module that returns the roots of non-linear equations.

Syntax

scipy.optimize.fsolve (func, x0, args=(), fprime=None, full_output=0, col_deriv=0, xtol=1.49012e-08, maxfev=0, band=None, epsfcn=None, factor=100, diag=None)

Parameters

• func: It is a function that takes an argument and returns the value.
• x0: ndarray, It is a starting estimate for the root of fun(x)=0.
• args: Tuple, it is an extra argument to the function, optional.
• fprime: It is a function to compute the Jacobian of function with derivatives.
• full_output: It is a boolean value and it is optional.
• col_deriv: It is a boolean value and it is also optional. Specify whether the Jacobian function computes derivatives down the columns
• xtol: It is float, optional.
• maxtev: It is int and the maximum number of calls to the function, optional.
• band: It is a tuple and optional parameter. If set to a two-sequence containing the number of sub- and super-diagonals within the band of the Jacobi matrix, the Jacobi matrix is considered banded 
• epsfcn: It is float and optional.
• factor: It is float and it determines the initial step bounds.
• diag: It is a scale factor for the variables.

Returns

• x: ndarray, It is a solution.
• infodict: It is a dictionary of optional values with the keys.
  • nfev number of function calls
  • njev number of Jacobian calls
  • fvec function evaluated at the output
  • fjac the orthogonal matrix
  • r upper triangle matrix
  • qtf the vector
• ier: An integer flag.
• msg: If no solution is found, mesg details the cause of failure.

Trending

[Fixed] typeerror can’t compare datetime.datetime to datetime.date

Code 1: To find the roots of an equation y+2cos(y) starting point – 0.2

from math import cos
import scipy.optimize
def fun(y):
    x = y + 2*cos(y)
    return x
x = scipy.optimize.fsolve(fun,0.2)
print (x)

• Using math function to import cos function.
• Importing scipy.optimize from that we will use fsolve.
• Creating a function. Inside a function giving an equation.
• Next using fsolve and giving the starting point of an equation.

Output

[-1.02986653]

Code 2: To find the roots of an equation 4sin(y) – 4 starting point 0.3

from math import sin
import scipy.optimize
def fun(y):
        x= 4*sin(y) - 4
        return x
x= scipy.optimize.fsolve(fun,0.3)
print (x)

• Using math function to import sin function.
• Importing scipy.optimize from that we will use fsolve.
• Creating a function. Inside a function giving an equation.
• Next using fsolve and giving the starting point of an equation.

Output

[1.57079633]

Code 3: To solve an equation with a starting point x0=2 and x1=2

from math import cos
import scipy.optimize
def fun(x):
        y = [x[1]*x[0] - x[1] - 6, x[0]*cos(x[1]) - 3]
        return y
x0 = scipy.optimize.fsolve(fun,[2, 2])
print(x0)

• Using math function to import sin function.
• Importing scipy.optimize from that we will use fsolve.
• Creating a function. Inside a function giving an equation.
• The starting point is 2 and 2.
• Next using fsolve and giving the starting points.

Output

[6.49943036 1.09102209]

Code 4: To solve an equations for x**2+y-4 and x+ y**2+3

import scipy.optimize
def fun(variables) :
    (x,y)= variables
    eqn_1 = x**2+y-4
    eqn_2 = x+y**2+3
    return [eqn_1,eqn_2]
result = scipy.optimize.fsolve(fun, (0.1, 1)) 
print(result)

• Importing scipy module.
• Creating a function. Inside a function we are giving to equations to solve.
• Giving a starting point as 0.1 and 1

Output

[-2.08470396 -0.12127194]

Trending

[Solved] runtimeerror: cuda error: invalid device ordinal

Code 5: Using fsolve and numpy to solve the equation

import numpy as np
import scipy.optimize as opt
def fun(var):
    x = var[0]
    y = var[1]
    z = var[2]
    Func= np.empty((3))
    Func[0] = x**2+y-20
    Func[1] = x**2+y+1
    Func[2] = x+y**2+3
    return Func
a= np.array([2,1,3])
b= opt.fsolve(fun,a)
print(b)

• Importing numpy and scipy.
• Creating a function
• Inside a function we are giving an equations
• Next creating an array to give the starting point.
• Using fsolve to solve a non linear equations

Output

[ 3.00891769e+00  1.83529872e-02 -1.81037724e+03]

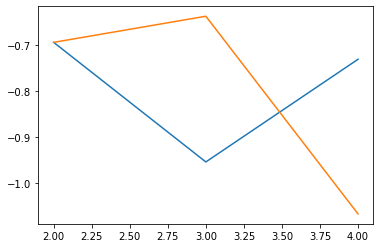
Interesting Code: Solving non-linear equation and a graph for it

import scipy.optimize 
import matplotlib.pyplot as plt
import numpy as np
def function(z,*args):
  x, y = z
  M= args[0] 
  return (x-M* np.exp(x+y),y-2* np.exp(x+y))
M= np.linspace(2,4,3)
X = []
Y =[]
for a in M:
  x,y = scipy.optimize.fsolve(function,(6.0, 6.0) ,args=(a))
  X.append(x)
  Y.append(y)
print(x,y)
plt.plot(M,X)
plt.plot(M,Y)

This code will display the additional information that is a graph. It will display the solution and a graph as a result.

Output

-0.7302656622876462 -1.0679579275975384

Trending

[Fixed] typeerror: type numpy.ndarray doesn’t define __round__ method

FAQs related to scipy fsolve

Conclusion

Here we have learned how to solve a nonlinear equation. We used the fsolve function to solve an equation. With that, we also learned how to plot a graph for that nonlinear equation. We hope this article is easy to understand. Learn coding with us!