Hello coders!! In this article, we will be learning about the Python bitonic sort algorithm and its implementation in Python. Sorting is the way of arranging the elements in a specific order, i.e., either in ascending or descending order.
Various sorting algorithms are available, all with pros and cons. The bitonic sort is a parallel sorting algorithm that sorts the elements through comparisons.
What is the Bitonic sort?
It is a sorting algorithm that runs parallel. In this algorithm, there are O(n2 log n) comparisons. Although there are more comparisons, it’s more suitable for parallel implementation because the elements are compared in a predefined sequence (the bitonic sequence) that doesn’t depend on data. Therefore, it is optimal for implementation in hardware and parallel processor array.
What is the Bitonic sequence?
In this sequence, the elements start decreasing after some particular index, whereas before that index, the elements come in increasing order.
x0 <= x1 …..<= xi and xi >= xi+1….. >= xn-1- A sequence in increasing order is said to be Bitonic, with the decreasing part being empty. Similarly, the decreasing sequence is said to be Bitonic, with the increasing part as empty.
- A Bitonic Sequence, when rotated, is also bitonic.
How to convert a Random sequence to a Bitonic sequence?
Let us first consider the following elements of an array

First, we will make pairs of elements. We will then create its bitonic sequence such that one is in ascending order, the other is in descending order, and so on.
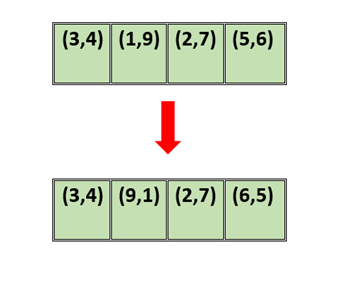
Now, we will make pairs of each pair such that every sequence has four elements.

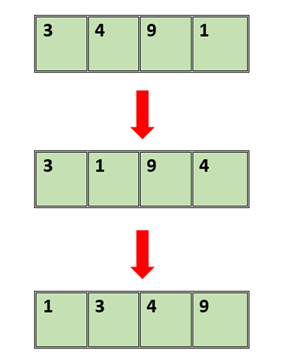
Sorting the first sequence in ascending order:
- First, compare the elements
- Then, compare the adjacent elements
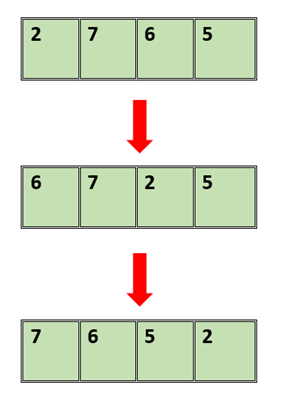
Similarly, we will sort the second sequence in descending order:
Now, we will merge these two to get our final bitonic sequence

Bitonic Sort Algorithm:
- At first, we will create a bitonic sequence.
- Next, we need to compare and sort the corresponding elements of both halves of the sequence.
- Now, we will compare and swap every second element of the sequence
- At last, we will compare and swap adjacent elements of the sequence
Illustration of Bitonic Sort Algorithm:
Let us consider the above-created bitonic sequence.
At first, we will compare and sort the corresponding elements of both halves of the sequence.
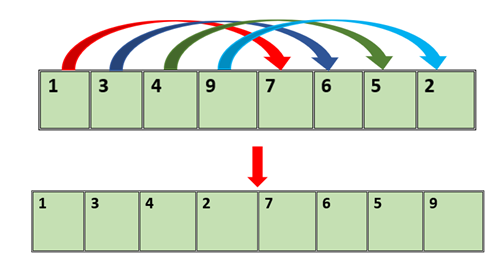
Now compare and swap every second element of the sequence
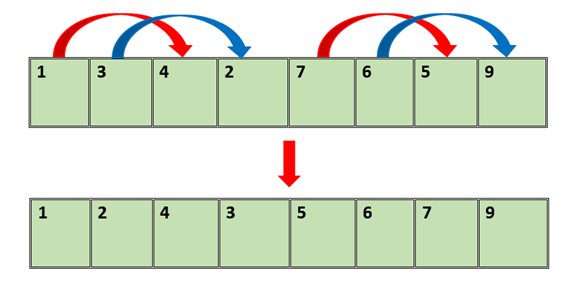
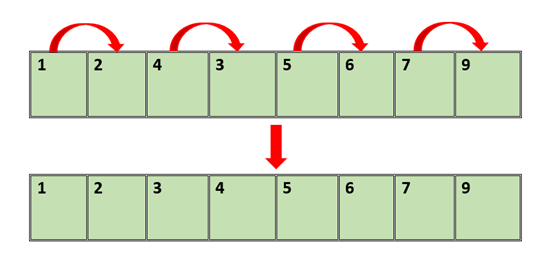
We will now do the same for the adjacent elements
Source Code in Python:
def compare_swap(a, i, j, d):
if (d == 1 and a[i] > a[j]) or (d == 0 and a[i] < a[j]):
a[i], a[j] = a[j], a[i]
def merge(a, l, cnt, d):
if cnt > 1:
k = int(cnt / 2)
for i in range(l, l + k):
compare_swap(a, i, i + k, d)
merge(a, l, k, d)
merge(a, l + k, k, d)
def bitonic_sort(a, l, cnt, d):
if cnt > 1:
k = int(cnt / 2)
bitonic_sort(a, l, k, 1)
bitonic_sort(a, l + k, k, 0)
merge(a, l, cnt, d)
def sort(a, N, u):
bitonic_sort(a, 0, N, u)
a = [3, 4, 1, 9, 2, 7, 5, 6]
n=len(a)
u = 1
sort(a, n, u)
print("\nSorted array is")
for i in range(n):
print("%d" % a[i])
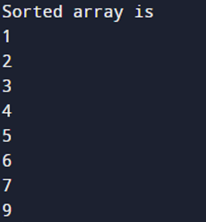
Output:
Complexity Analysis:
- Time complexity: O(log 2 n)
- Space complexity: O(n log 2 n)
Advantages:
- Memory is well handled by the process
- Best suited for parallel processor array
Bitonic Sort vs Merge Sort:
| Bitonic Sort | Merge Sort |
| Comparison based parallel algorithm | Divide and conquer algorithm |
| O(n Log 2n) comparisons are done | O(nLogn) comparisons are done |
| smaller numbers of each pair are moved to the left and larger numbers to right. | input array is divided into two halves and then the function calls itself for the two halves, and ultimately the sorted halves are merged |
| Time complexity: O(log 2 n) | Time complexity: O(nLogn) |
Must Read
- TimSort: Algorithm and Implementation in Python
- Pigeonhole Sort in Python With Algorithm and Code Snippet
- Understanding Strand Sort in Python With Example
- Shell Sort Algorithm and Program in Python
- Understanding Python Bubble Sort with examples
- Insertion Sort in Python [Program, Algorithm, Example]
Conclusion:
All sorting algorithms have their own pros and cons. Even though the number of comparisons in bitonic sort python is more, it is best suited for parallel arrays.
However, if you have any doubts or questions, do let me know in the comment section below. I will try to help you as soon as possible.
Happy Pythoning!

![[Fixed] typeerror can’t compare datetime.datetime to datetime.date](https://www.pythonpool.com/wp-content/uploads/2024/01/typeerror-cant-compare-datetime.datetime-to-datetime.date_-300x157.webp)
![[Fixed] nameerror: name Unicode is not defined](https://www.pythonpool.com/wp-content/uploads/2024/01/Fixed-nameerror-name-Unicode-is-not-defined-300x157.webp)
![[Solved] runtimeerror: cuda error: invalid device ordinal](https://www.pythonpool.com/wp-content/uploads/2024/01/Solved-runtimeerror-cuda-error-invalid-device-ordinal-300x157.webp)
![[Fixed] typeerror: type numpy.ndarray doesn’t define __round__ method](https://www.pythonpool.com/wp-content/uploads/2024/01/Fixed-typeerror-type-numpy.ndarray-doesnt-define-__round__-method-300x157.webp)