Min Heap In Python And Its Operations

In this article, we are going to learn about min heap in python in a detailed manner. Here we will learn What is a heap? What is min heap in python? Time complexity and applications of a heap. And at last, we will see the difference between min and max heap. Let us start now!

Min heap is one of the types of heap. Heap has two types: min heap and max heap. Heap is a data structure. Generally, a heap is like a tree that has many nodes. In a heap, the last node may be empty or filled. In a heap, there are two nodes parent node and child node. A heap is also known as a binary heap. In a max heap, a parent node is always greater than or equal to the child node. And in a min-heap, a parent node is always lesser than or equal to a child node.

Contents

What is min heap in python?

A min heap is a heap that contains nodes. It is one of the types of the heap. In min heap, there are two types of nodes. A parent node or root node and a child node are the types of nodes in a heap. A parent or root node should always be lesser or equal to the child node in the min heap. If the parent node is greater than a child node, then a heap becomes the max heap. In min heap, the priority is always to the smallest element. It follows the ascending order.

Example for min heap

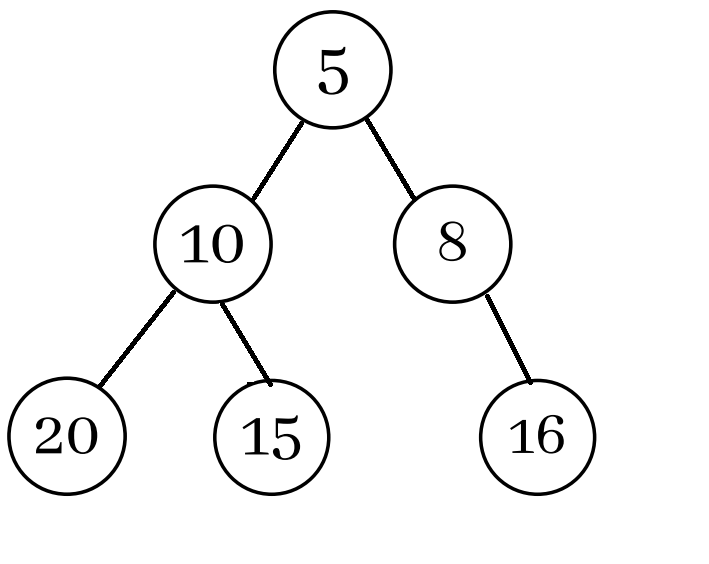
We can see that none of the parent nodes is greater than the child node. So this is the perfect example for min heap. If this condition is not followed, then it is not a min heap.

Implementation of min heap in python using library functions

import heapq as heap
l=[ ]
heap.heappush(l,20)
heap.heappush(l,14)
heap.heappush(l,9)
heap.heappush(l,90)
heap.heappush(l,30)
heap.heappush(l,40)
print("The heap is:",l)
print("The parent node is:",heap.heappop(l))
print("The child nodes are:",l)

Here we are generating a min heap using a heapq library. Using all the operations to generate a min heap. It will give the result as which is the parent and which is the child node. And also, it will give the minimum value of the heap so that we can know which is the parent node from that.

Output

The heap is: [9, 20, 14, 90, 30, 40]
The parent node is: 9
The child nodes are: [14, 20, 40, 90, 30]

Representation of min heap in python

We all know that the min heap is a binary tree. An array always represents a min heap. array[0] is the root element in the min heap.

Parent node representation

array[(i -1) / 2]

Left child node representation

array[(2 * i) + 1]

Right child node representation

array[(2 * i) + 1]

What are the operations are available in min heap?

getMin()
extractMin()
insert()

getMin() operation

It is useful to return the parent node of the min heap.
O(1) is the time complexity of getMin().

extractMin() operation

This operation removes the minimum element from the min heap.
O(Log n) is the time complexity of extractMin() operation
extractMin() maintains the heap property after removing the parent node.

insert() operation

This operation is useful to insert a new node at the end of the heap.
If the new child node is smaller than a parent node then we have to exchange the parent node and the child node.
O(Log n) is the time complexity to add the new node in the heap.

Implementation of min heap in python without using any library functions

import sys
class minheap: 
    def __init__(self, size):
        self.storage=[0]*size
        self.size = size
        self.heap_size = 0
        self.Heap = [0]*(self.size + 1)
        self.Heap[0] = sys.maxsize * -1
        self.parent = 1
        self.root=1
    def getParentIndex(self,index):
        return (index-1)//2
    def getLeftChildIndex(self,index):
        return 2*index+1
    def getRightChildIndex(self,index):
        return 2*index+2
    def hasParent(self,index):
        return self.getParentIndex(index)>=0
    def insert(self,index):
        if self.heap_size >= self.size :
            return
        self.heap_size+= 1
        self.Heap[self.heap_size] = index
        heap = self.heap_size
        while self.Heap[heap] < self.Heap[heap//2]:
            self.swap(heap, heap//2)
            heap = heap//2
    def swap(self, left, right):
        self.Heap[left], self.Heap[right] = self.Heap[right], self.Heap[left]
    def root_node(self, i):
        if not (i >= (self.heap_size//2) and i <= self.heap_size):
            if (self.Heap[i] > self.Heap[2 * i]  or  self.Heap[i] > self.Heap[(2 * i) + 1]): 
                if self.Heap[2 * i] < self.Heap[(2 * i) + 1]:
                    self.swap(i, 2 * i)
                    self.root_node(2 * i)
                else:
                    self.swap(i, (2 * i) + 1)
                    self.min_heapify((2 * i) + 1)
    def getMin(self):
        min_value = self.Heap[self.root]
        self.Heap[self.root] = self.Heap[self.root]
        self.size-= 1
        self.root_node(self.root)
        return min_value
    def extractMin(self):
        data=self.Heap[1]
        self.Heap[1]=self.Heap[self.size-1]
        self.size-=1
        return data
    def main(self):
       for i in range(1, (self.heap_size//2)+1):
            print("Parent Node:",str(self.Heap[i]),"Left Node:"+str(self.Heap[2 * i]),"Right Node:",str(self.Heap[2 * i + 1]))
minHeap = minheap(11)
minHeap.insert(70)
minHeap.insert(8)
minHeap.insert(80)
minHeap.insert(3)
minHeap.insert(90)
minHeap.insert(30)
minHeap.insert(23)
minHeap.insert(45)
minHeap.insert(100)
print("The Root element is " ,(minHeap.getMin()))
minHeap.main()
print("Remove node ", minHeap.extractMin())
minHeap.main()

We are creating a min heap using python. Using all the operations to generate a min heap. It will give the result as which is the parent and which is the child node. And also, it will give the minimum value of the heap so that we can know which is the parent node from that.

Output

The Root element is  3
Parent Node: 3 Left Node:8 Right Node: 23
Parent Node: 8 Left Node:45 Right Node: 90
Parent Node: 23 Left Node:80 Right Node: 30
Parent Node: 45 Left Node:70 Right Node: 100
Remove node  3
Parent Node: 100 Left Node:8 Right Node: 23
Parent Node: 8 Left Node:45 Right Node: 90
Parent Node: 23 Left Node:80 Right Node: 30
Parent Node: 45 Left Node:70 Right Node: 100

Applications of heap

k-way merge using heap data structure.
Graph algorithm like prim’s algorithm using heap data structure.
Useful for job scheduling algorithm
While implementing priority queue heap data structure is the major one.
Useful for order statistics

Difference between min heap and max heap

min heap	max heap
The parent node is always lesser than or equal to a child node.	The parent node is always greater than or equal to a child node.
The parent node is always a smaller element.	The parent node is always a larger element.
It is in ascending order.	It is in descending order.
The first priority is always to the smallest element.	The first priority is always to the largest element.

1. What is the major condition in the min heap?

In min heap, the parent node is always lesser than or equal to a child node.

2. What are the types of the heap?

Heap is of two types. They are min heap and max heap.

3. Which element has the highest priority in the min heap?

The smallest element in the node has the highest priority in the min heap.

Conclusion

Here we have come to the end of an article. We have learned a lot of the things about min heap in python. Heap is a data structure that has a lot of applications. We hope this article is beneficial and easy to understand.