“Sorting Techniques Using Python“- A Sorting Algorithm is used to rearrange a given array or list elements according to a comparison operator on the elements. The comparison operator decides the new order of elements in the respective data structure.
Sorting is a skill that every software engineer and developer needs some knowledge of. Not only to pass coding interviews but as a general understanding of programming itself. The different sorting algorithms are a perfect showcase of how algorithm design can have such a strong effect on program complexity, speed, and efficiency.
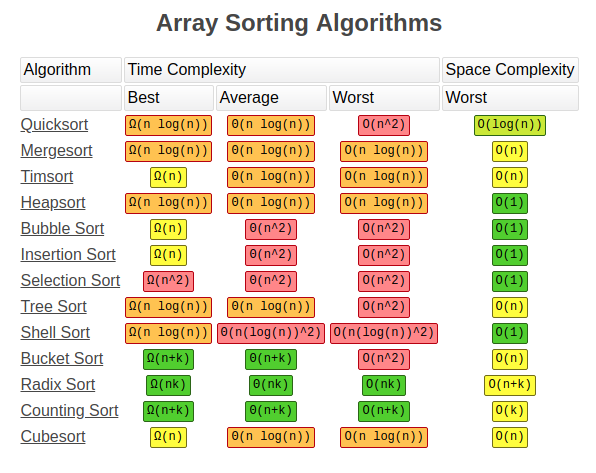
Some of the sorting techniques are:
1- Selection Sorting Techniques Using Python
The selection is one of the most used Sorting Techniques Using Python. This algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from the unsorted part and putting it at the beginning. The algorithm maintains two subarrays in a given array.
1) The subarray which is already sorted.
2) Remaining subarray which is unsorted.
In every iteration of the selection sort, the minimum element (considering ascending order) from the unsorted subarray goes to the sorted subarray.
Flowchart

Python code / Implementation :
def insertion_sort(nums):
for i in range(1, len(nums)):
item_to_insert = nums[i]
j = i - 1
while j >= 0 and nums[j] > item_to_insert:
nums[j + 1] = nums[j]
j -= 1
nums[j + 1] = item_to_insert
# Verify if it works
random_list_of_nums = [9, 1, 15, 28, 6]
insertion_sort(random_list_of_nums)
print(random_list_of_nums)
2- Bubble Sort
Bubble sorting algorithm iterates over a list, comparing elements in pairs and swapping them until the larger elements “bubble up” to the end of the list, and the smaller elements stay at the “bottom”.
We start by looking at the initial two components of the rundown. On the off chance that the principal component is bigger than the subsequent component, we swap them. In the event that they are as of now all together we leave them in its present condition. We at that point move to the following pair of components, look at their qualities and swap as important. This procedure proceeds to the last pair of things in the rundown.

Upon reaching the end of the list, it repeats this process for every item. Obviously, to optimize the algorithm, we need to stop it when it’s finished sorting.
How would we know that we’re finished sorting? If the items were in order then we would not have to swap items. So, whenever we swap values we set a flag to True to repeat sorting process. If no swaps occurred, the flag would remain False and the algorithm would stop.
Python Code / Implementation :
def bubble_sort(nums):
swapped = True
while swapped:
swapped = False
for i in range(len(nums) - 1):
if nums[i] > nums[i + 1]:
nums[i], nums[i + 1] = nums[i + 1], nums[i]
swapped = True
# Verify if it works
random_list_of_nums = [5, 2, 1, 8, 4]
bubble_sort(random_list_of_nums)
print(random_list_of_nums)
3- Insertion Sorting Techniques Using Python
Insertion sorting algorithm is one of the popular Sorting Techniques Using Python. Here, the algorithm segments the list into sorted and unsorted parts. It iterates over the unsorted segment, and inserts the element being viewed into the correct position of the sorted list.
We expect that the principal component of the rundown is arranged. We at that point go to the following component, we should call it x. In the event that x is bigger than the primary component we leave in its present condition. On the off chance that x is littler, we duplicate the estimation of the principal component to the subsequent position and afterward set the main component to x.
As we go to the other elements of the unsorted segment, we continuously move larger elements in the sorted segment up the list until we encounter an element smaller than x or reach the end of the sorted segment, and then place x in it’s correct position.
Python Code / Implementation :
def insertion_sort(nums):
for i in range(1, len(nums)):
item_to_insert = nums[i]
j = i - 1
while j >= 0 and nums[j] > item_to_insert:
nums[j + 1] = nums[j]
j -= 1
nums[j + 1] = item_to_insert
# Verify if it works
random_list_of_nums = [9, 1, 15, 28, 6]
insertion_sort(random_list_of_nums)
print(random_list_of_nums)
4- Quick Sort
Quick Sort begins by partitioning the list – picking one value of the list that will be in its sorted place. This value is called a pivot. All elements smaller than the pivot are moved to its left. All larger elements are moved to its right.

Knowing that the pivot is in it’s rightful place, we recursively sort the values around the pivot until the entire list is sorted.
Python Code / Implementation :
def partition(arr,low,high):
i = ( low-1 ) # index of smaller element
pivot = arr[high] # pivot
for j in range(low , high):
if arr[j] < pivot:
i = i+1
arr[i],arr[j] = arr[j],arr[i]
arr[i+1],arr[high] = arr[high],arr[i+1]
return ( i+1 )
def quickSort(arr,low,high):
if low < high:
pi = partition(arr,low,high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
# Verify if it works
random_list_of_nums = [22, 5, 1, 18, 99]
quick_sort(random_list_of_nums)
print(random_list_of_nums)
5- Merge Sorting Techniques Using Python
Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See following C implementation for details
We recursively split the list in half until we have lists with size one. We then merge each half that was split, sorting them in the process.
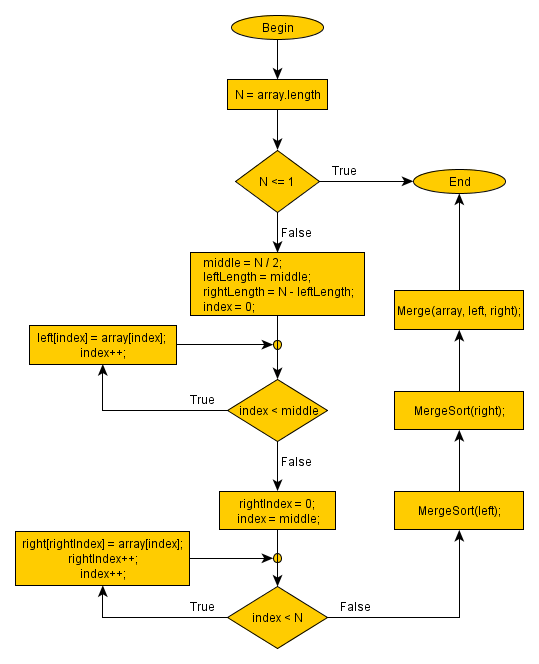
Sorting starts with comparing the smallest elements of each half. The first element of each list is the first to compare. If the first half begins with a smaller value, then we add that to the sorted list. We then compare the second smallest value of the first half with the first smallest value of the second half.
Every time we select the smaller value at the beginning of a half, we move the index of which item needs to be compared by one.
Python Code / Implementation :
def mergeSort(arr):
if len(arr) >1:
mid = len(arr)//2 #Finding the mid of the array
L = arr[:mid]
R = arr[mid:]
mergeSort(L)
mergeSort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i+=1
else:
arr[k] = R[j]
j+=1
k+=1
while i < len(L):
arr[k] = L[i]
i+=1
k+=1
while j < len(R):
arr[k] = R[j]
j+=1
k+=1
def printList(arr):
for i in range(len(arr)):
print(arr[i],end=" ")
print()
if __name__ == '__main__':
arr = [12, 11, 13, 5, 6, 7]
print ("Given array is", end="\n")
printList(arr)
mergeSort(arr)
print("Sorted array is: ", end="\n")
printList(arr)
# Verify it works
random_list_of_nums = [120, 45, 68, 250, 176]
random_list_of_nums = merge_sort(random_list_of_nums)
print(random_list_of_nums)
So, the above are some of the popular sorting techniques in Python. Sorting and listing makes take object oriented and helps to implement and run codes easily. Hence, sorting technique are very important.
