Hello coders!! In this article, we will explore and learn the coding of the game Tower of Hanoi in python. At first, we will learn about the game rules and then see the step by step implementation of the game in python. Without wasting any time, let’s dig into it.
What is the Tower of Hanoi in Python?
It is a mathematical puzzle game in which we use three identical rods and n disks, all of the different sizes. The discs are arranged in the first rod, such that the largest disc is placed at the bottom and the smallest at the top. To solve the puzzle, one needs to arrange the disc in the same order in the last rod via the middle rod.
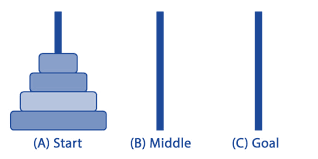
Rules of Tower of Hanoi in Python:
- We can move only one disc at any given time
- Only the disc which is at the top can be moved and placed ontop at any other rod
- A disc can be placed on top of a bigger disc only
An illustration of the Game:
Let us consider that initially there are 3 discs arranged as follows:
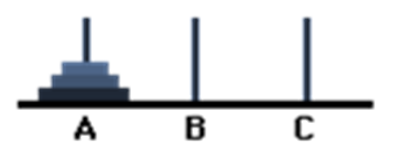
At first, we will move the disc from A to C
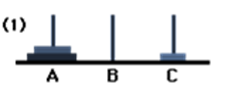
Now, we will move the disc from A to B
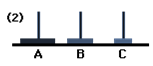
Next, we will move the disc of rod C to B
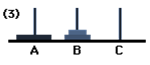
After this, we will move the disc from A to C
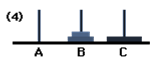
Now, move the disc from B to A
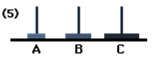
Next, we need to move the disc of rod B to C

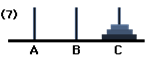
And for the last step, we will move the disc form A to C, thus solving the puzzle
Implementation of Tower of Hanoi in Python:
def tower_of_hanoi(numbers, start, auxiliary, end):
if(numbers == 1):
print('Move disk 1 from rod {} to rod {}'.format(start, end))
return
tower_of_hanoi(numbers - 1, start, end, auxiliary)
print('Move disk {} from rod {} to rod {}'.format(numbers, start, end))
tower_of_hanoi(numbers - 1, auxiliary, start, end)
numbers = 3
tower_of_hanoi(numbers, 'A', 'B', 'C')
Output:

Explanation:
- Here, we have used recursive method for the implementation of the game
- The function TowerOfHanoi() takes four parameters
- Number of discs
- Source rod
- Auxiliary rod
- Destination rod
- It first checks the condition if the number of disc is 1, it directly moves it to the Destination rod and terminates the function
- Then, we have recursively called the function to move the remaining n-1 discs from source node to the auxiliary node, using the destination rod as the auxiliary
- After that, the 1 disk that is remaining is directly moved from the source rod to the auxiliary rod
- Lastly, we have again recursively called the the function to move the remaining n-1 rods from the auxiliary rod to the destination rod, using the source node as auxiliary
Is it possible to solve Tower Of Hanoi without recursion?
This question can pop into anyone’s mind. Well, it is definitely possible. The tower of Hanoi problem can be solved non recursively as well by a binary solution approach where the n number of discs is encoded and represented in binary form of numbers 0 – 2^n.
Time complexity for the recursive solution:
The time complexity for the recursive solution of Tower of Hanoi is O(2^n), where n is the number of discs.
Must Read
- Best Career Options With Python
- Rock Paper Scissors Game Development in Python
- Understanding Strand Sort in Python With Example
Conclusion:
In this article, we learned in detail about the game of Tower of Hanoi and learned its recursive implementation in Python. We also elaborated the game concept in detail and finally saw an easy python code to implement it.
However, if you have any doubts or questions, do let me know in the comment section below. I will try to help you as soon as possible.
Happy Pythoning!

Therre is an error. You can’t moving the third disk on the rod C because there’re already the other disks
Hi, thank you for pointing it out. Seems like there was a minor mistake in the code.
I’ve updated the code with correct logic and better name convention. Hope it helps!
Moves 1 to 7: A to C, A to B, C to B, A to C, B to A, B to C and A to C. This is not what the program returns
Correct